I'd like to share some of the amazing range of rhythms you can find, linking music and maths, some discovered only in the last few years. These include: fibonacci gamelan patterns - highly structured yet the pattern of beats never repeats; the rhythm you get if two musicians each with perfectly steady rhythm play as out of time as possible; the rhythm of the famous "Cantor's set"; and the fairly recent discovery that many rhythms of music throughout the world are "Euclidean rhythms" - uneven beat patterns pleasing to the ear made with a surprisingly simple construction.
You may well find rhythms here you've never heard before. I thought I'd share some of them with you, using videos from the program I wrote to help explore them, Bounce Metronome and talk about the maths behind them.
These are different rhythms - the out of time drummers rhythm is towards the end of this article.
I'll have quite a few equations here, for those who find maths fun (nothing too complicated). But it will be easy to skip the maths for those who don't enjoy it so much.
FIBONACCI GAMELAN PATTERNS
"What's the best tuning for consonance, beauty, relaxation and peace. I don't want dissonance or tension that needs to resolve.".
That was Jesse Thom's interesting question some time back at the Xenharmonic Alliance in facebook,
My idea was to take any very restful unchanging harmony - there are lots of possible choices, including the unison, but one natural choice is the harmonic series - and then use rhythms to maintain the interest.
My first thought was to use polyrhythms for the rhythmic interest, as in the harmonic polyrhythms of Bounce Metronome and the Lambdoma music therapy, as in the last article here.
But then I thought, what about the Fibonacci rhythms? So this is the result.
These fascinating rhythmic patterns are highly structured but have no repeating measure. There is no repeating pattern at any time scale. There must be a million different ways to approach her question, this is just one idea :)
I thought this was a fun place to start - it's one of the rhythms of David Canright, inspired by rhythmic patterns of gamelan music. They also have a connection with Roger Penrose's non periodic tilings. His original paper is here Fibonacci Gamelan Rhythms
They work very like the Tune Smithy sloth canons and the Per Nørgård sequence, whcih I talked about before, that every row plays the same rhythm at a different speed, but this time, it's for another reason.
Starting from the slowest voice, and working up to faster voices, it works like this, where L means a long beat for that voice, and S means a short beat:
L (slow) = L + S (faster)
S (slow) = L (faster).
Each row plays the rhythm a little faster, but all the rows are playing the same pattern of beats L S L L S L S L ...(for as far as it goes for the row). Also, whenever one of the slower voices plays a note, all the faster voices come together to play one of their notes at the same moment.
The interesting thing about this rhythm is that it never repeats, ever. Larger and larger chunks of it reappear in the pattern over and over again - but the whole pattern never repeats.
This makes it a non periodic, or aperiodic pattern to mathematicians. Though we used only a finite number of layers in this pattern, the original mathematics works by continuing this process to endlessly many row, so you end up with a never repeating but endlessly played rhythm, identical in all the parts.
Now, to make all the rhythms identical, we are going to make a very special choice for the length of the L and the S beats. We need the ratio of the long beat to the short beat has to be the same in each row.
A little mathematics will give us the answer we need
First, we have an r with:
L*r = L + S
S*r = L
where r is the amount by which each row is faster than the next one.
From this one can figure out that
L*r = L + L/r
so r = 1 + 1/r.
A mathematician will instantly recognise this as the defining equation for the golden ratio, so our answer is, that the ratio L/S is the golden ratio.
This rhythm is used in the study of Penrose tilings, and in this field, is known as the "musical sequence".
As far as I know, that's a complete coincidence - mathematicians (in this case John Conway who named the sequence) often use names like this in their theories not necessarily suggesting any non-mathematical significance. It is just a way to make abstract ideas easier to remember, and you can call them just about anything.
But now we find that there is a musical connection after all.
It's also connected with the Penrose tiling.

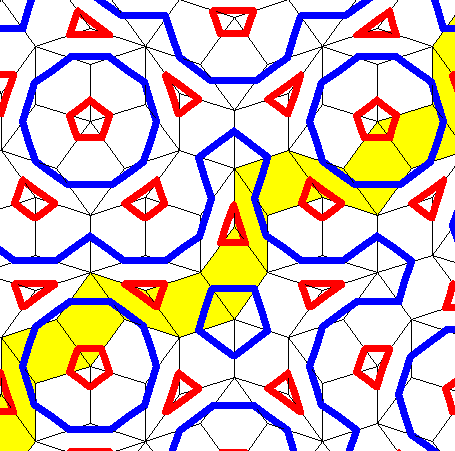
Roger Penrose standing on a floor tiled with his tiling.
Let's look at a patch of this tiling - it comes in several forms but one version is made up of two types of rhombus - broad and narrow. In this picture, they are shown with red and blue markings on them, and you have to fit them together so that the red and blue lines continue without a break from one tile to the next.
You can prove that you can fit the tiles together in this way to cover the entire surface of the plane, without gaps or overlaps - but that there is no way to do that which creates a repeating pattern. You find larger and larger patches that repeat, for instance the star arrangement of five broad rhombs surrounded by five narrow ones - but the whole pattern never repeats. For instance there is no way you could make this into repeatng wallpaper.
Then the connection with the musical sequences is, that if you take any singe row of rhombi, connected each to the next parallel edge to parallel edge, like the one marked in yellow in this picture.
For instance, the yellow line shown in the diagram above goes, from bottom left, L, S, L, L, S, L,L, S, L, S, L, L, S, which is a fragment of a Fibonacci gamelan pattern.
It doesn't matter which row you choose in which direction - they all trace out these fibonacci gamelan pattern rhythms with the pattern of wide and narrow rhombs.
For maths geeks, there's a fun connection with the geometry of five dimensions of space. We all know the way you can show a slice through a cubic lattice (pile of stacked blocks) like this, the Rhombille tiling:
Here the lines show the "dual tiling" of hexagons and triangles
Well do the same thing in five dimensions, choose the angle just right for your cut, and the result is a Penrose tiling. This is a result by De Bruijn, and his idea helped lead to new generalizations of the Penrose tilings. The lines in this drawing also generalize into higher dimensions as the "n-grid duals" used in De Bruijn's construction.
So, that's the origin of these rhythms in Penrose tilings. But now we can do things with them for the purposes of music.
One idea due to David Canright is to arrange the beats by flipping the L and S if necessary so that the L is closest to the most deeply reinforced beat (the one with most instruments playing simultaneously) - the result may sound better musically.
Then - no need to restrict ourselves to that L to LS and S to L substitution. You can get similar interesting results with other substitutions, including more than two beat sizes. It's an idea you can develop in many different directions. I've got tools you can use to do this in Tune Smithy, to create more Fibonacci rhythms with up to three beat sizes, any substitution rule you like
Try these "non repeating bongos" for instance. Many more examples from Tune Smithy here. (It's from many years ago - the sounds are a bit basic, just the default sounds for the Roland sound canvas software - must do a new update some time with some of the wonderful instrument sounds available easily to anyone nowadays).
CANTOR'S DUST FRACTAL AS A RHYTHM
This is another way to make a rhythm with a lot of structure, which doesn't repeat, by using a fractal rhythm. The idea is to have the same rhythm nested inside of itself endlessly.
You can make many rhythms like this in Tune Smithy but I thought I'd share this one, which is connected to the famous Cantor's set.
The lowest points in this rhythm, the double taps within double taps within double taps, play out the rhythm of Cantor's set. I'll put the details into a separate article (was here).
The Cantor's set is a fractal, a fractal with an exact similarity in fact, any detail of the set looks like the whole thing. So this is a fractal rhythm.
Actually, I've arranged the pitches here so that it is also an exact fractal in the pitch / time domain. To make that work, the pitches have to get closer together as they get higher.
This by the way is played in my Tune Smithy, while most of the other programs on this page are in Bounce Metronome.
Indeed, what it played is the Number of 1's in ternary (base 3) expansion of n (entry in the On Line Encyclopedia of Integer Sequences). 0, 1, 0, 1, 2, 1, 0, 1, 0, 1, 2, 1, 2, 3, 2, 1, 2, 1, 0, 1, 0, 1, 2, 1, 0, 1, 0, 1, 2,...
Here is what it looks like if you plot it out as a graph
 The lowest points there correspond to the points left behind in Cantor's dust construction after you remove the middles of all the lines.
The lowest points there correspond to the points left behind in Cantor's dust construction after you remove the middles of all the lines.
Now - it's an approximation of course. You can't count through all the numbers in a line sequentially like that. But then our ears can't discriminate notes that are very close together either.
So, think of it as, for instance, the number of 1s in the first few digits of the ternary expansion of the time so far What you hear in the lowest taps is indeed the rhythm of Cantor's dust - but think of it that every one of the low note taps you hear with the ear is also divided further into even smaller double taps, and those into yet more, way beyond the resolution of our hearing.
WHY MATHEMATICIANS ARE FASCINATED BY CANTOR'S SET
This is a little mathematical aside for those who find maths fun. If you are mainly interested in the rhythms themselves just skip ahead to the next section.
Let's just look at the line from zero to one, as it's easiest to see things that way.
First, you can show that it has as many points as the original line.
Why it has as many points as the original line: Look at the way the numbers are defined, as sequences of 0s and 2s in ternary, then if you replace the 2s by 1s, each of those can be matched up with a sequence of 0s and 1s in binary - this gives a proof that it has as many points as there were in the original line. That's not too paradoxical since points are of zero size except
You can also show that it has total length zero - that's reasonably intuitive - it looks so sparse, and is easy to prove rigorously. Let's just look at it from zero to one, that's easy to prove.
Why it has zero total length. Look at how it is constructed, take the line between 0 and 1 for instance. Well you remove a third of it, leaving 2/3. Then you remove a third of what is left, so a third of 2/3, i.e. 2/9, leaving 4/9. Then leave a third of that, 4/27, leaving 8/27. Keep repeating that process, next stage leaves 16/81, general term is 2n/3n, and you find the amount left keeps going down to zero.
So you have removed the entire length of the original line, so it has zero total length, just like a finite scattered set of points.
If you double the length of a line, not too surprising if it has the same number of points, as points are of zero length. The only way that could make a difference is if the points were finite in size.
But, a line of zero length with the same number of points as a line of length 1? Well it seems it can.
Georg Cantor who discovered the Cantor set with all these paradoxical properties - as well as many other paradoxical results about set theory.
Then, there's another paradoxical result about the way the points are distributed.
Paradox about density of Cantor's set. Normal ratios are "dense" - no matter where you are on the line, you'll find a good approximation, as close as you like, with ratios.
Cantor's set however, you can see quite easily, is "nowhere dense" - you can find patches of the line with no points arbitrarily close to any of the points in the set to either side.
That would be fine, except, you can also show in a mathematically rigorous way, that it is "uncountable". You can list all the ratios one after another, but any attempt to list all the points in the Cantor's set will always leave some of them out. It's a simple proof. How can that be?
How can a set which has so many gaps in it, gaps everywhere, have more points than a set with no continuous gaps at all?
These are all considered to be mathematically rigorous proofs. But the results are rather paradoxical, according to everyday ways of thinking.
This is just one of many paradoxical things in modern mathematics - paradoxical but thought to be valid mathematics. For more examples, see the Paradoxes of Set Theory.
It's all a bit puzzling. These results puzzled all the mathematicians in the early twentieth century.
Motivated by these strange, almost nonsensical seeming results, then back early in the twentieth century, Hilbert, great mathematician of his time with a truly vast compendious knowledge of maths started a great enterprise and program to finally show that our mathematics is rigorous and consistent, called "Hilbert's program",
David Hilbert, the mathematician who set out a great program to try to prove once and for all that mathematics is consistent
But in the 1930s, Godel in a famous, surprising, and shocking discovery (at the time) showed that any theory that has all the finite numbers in it with addition and multiplication and (was later shown, in "Robinson arithmetic") hardly anything else, can never be proved to be a consistent theory. This is really basic unsophisticated maths, things that anyone who can add and multiply would accept to be true without question.
Kurt Gödel, the mathematician who proved rigorously that David Hilbert's program can never succeed. That (as it later turned out) you can't even prove that the simple rules we use for addition and multiplication are consistent.
Anyway - the maths behind these ideas is generally thought to be rigorous and consistent if not provably so. But it's not so easy to understand philosophically
EUCLIDEAN RHYTHMS IN WORLD MUSIC
This is based on a surprising discovery by Godfried Toussaint a few years ago that many irregular rhythms in music world wide, complex measures mixing eg. 2 and 3 beat patterns, can be got by a simple algorithm that just spreads the notes out as evenly as possible within the measure.
This is one of them. It's the result of spreading 5 hits as evenly as possible over 13 beats.
"E(5,13) = [x . . x . x . . x . x . .] = (32323) is a Macedonian rhythm which is also played by starting it on the fourth onset as follows: [x . x . . x . . x . x . .]"One of the rhythms from.Godfried Toussaint's landmark paper in 2005, The Euclidean Algorithm Generates Traditional Musical Rhythms
This is a Macedonian rhythm apparently. He found a huge range of different rhythms from around the world, often the same rhythm used in many different musical cultures, all of which were these Euclidean rhythms..
RHYTHM PHASING
This is the same rhythm with rhythm phasing - played twice, and the two versions go in and out of phase with each other. I've also done it with the tempo going faster and faster.
This is a technique that Steve Reich explored in some of his music, such as his Piano Phase.
Here is his Piano Phase played on Marimba, for a change (it's usually on piano, easy to find videos of those).
And here is a rhythm played in 8 different parts in Bounce Metronome, all played at slightly different tempi:
NESTED AND FRAGMENTARY TUPLETS
It's a tuplet if you play for instance three notes in the space of two (or four) or five notes in the place of four etc.
Triplets especially are common in most styles of music. But you can get much more complex rhythms than that.
For instance, what if you break off one of the tuplets before it's finished, and start again, and put that into a loop? And then do that with several tuplets simultaneously?
This is the result.
Then what about nesting tuplets one inside each other?
Part 2, the red notes, plays a triplet for the first two notes of 3/4Nested tuplets are used for instance in Frank Zappa's Black page - and you can get much more complex than that in some classical music - such as Brian Ferneyhough's quartet number 3 movement 2 which goes up to 4 levels of nesting tuplets!
Part 1, blue notes, plays a quintuplet within the first note of the red triplet, and then a triplet inside of the second note of the red triplet.
Part 3 plays a triplet, but the other way around from part 2, a whole note followed by a triplet
Part 4 plays straight quarter notes.
Though the bounce shows it as 15 and 9-tuplets, it was entered as music notation as a quintuplets and triplets inside a triplet.
This is a fairly simple rhythm as such things go, but shows the idea.
SYNCOPATED POLYRHYTHMS OF AFRICAN MUSIC
Polyrhythms are quite straight forward to understand (if not to play). Before I present it though, be aware, there are two different ways this word is used. Sometimes it means several rhythms played at once, all with beats of the same size, but each rhythm repeating after a different number of beats.
But most often, that's called a polymeter, and a polyrhythm is something like this:
There you have two beats per measure played with the blue part. The red part plays seven beats in the same time as the two blue beats. Then the purple part plays three beats in the same time as the two and three beats in the other parts.
The usual convention is to use colons between the numbers to describe a polyrhythm, so this is the 7:3:2 polyrhythm.
So, they do all start exactly together and end together. What if they don't all start together at the same place in the measure?
That's the idea of the African syncopated polyrhythms.
This video shows a 4:3 polyrhythm, played on the red and blue bouncing balls - but with the parts shifted each by half a beat so they don't coincide ever. The red and cyan bounces emphasize one each of the syncopated beats to highlight the syncopated effect.
And this is the same idea, syncopated 4:3, except, I've shifted all the parts to all possible positions in a similar kind of way - the idea is that the 4 and 3 beats instead of meeting each other at the measure beat can meet each other at any of each other's beats in the measure. Try that out in all possible ways and you get this rhythm
MORPHING POLYRHYTHMS
Another fun thing to try (rather hard to perform) is a morphing polyrhythm, to gradually morph from one polyrhythm to another.
This shows the idea, it does it in discrete steps, changes every few measures. You could also morph smoothly from one to the next, but I don't have that as an option in my program sadly
Why it can't change smoothly - in Bounce Metronome, you can have a different tempo in each part, as in the rhythm phasing examples, and you can morph the tempo gradually, also, but you can't adjust the tempo gradually in different directions in several parts at once. That is just a restriction of how I did the programming, result of a choice I made many years ago, when I didn't realize I'd need to be able to do this. Any rhythm phasing metronome I write again from scratch will be able to do this, and who knows, may find a way to add it in the future, but right now I can't, not easily without a lot of work.Anyway this is fun also, notice how the red ball plays five beats to a measure throughout. But the blue ball goes through several different rhythms all the way from 3 to 8 beats to a measure, with fractional beats per measure in between.
BUZZ ROLLS PLAYED AS POLYRHYTHMS
This is also rather fun. A buzz roll is when you let the drum stick bounce lightly but fast, faster and faster through the roll.
Here is Vic Firth demostrating a buzz roll
So, what about a slow polyrhythmic buzz roll, or multiple bounce roll. What would that sound like. Here we go:
THE HO HO CHI RHYTHMS
This is another fun thing you can do, have beats all the same, but the measures differ, and you get something like this
This is first of the Ho Ho Chi rhythms of Andy Hodges, who has made them into a progressive course and book going through all the possible rhythms like this up to a certain number of divisions. I think it must be the most thorough exploration made of these types of rhythms.
Eventually, keep going, and the two measures come together again.
Here is another example
MEASURES AND BEATS BOTH DIFFERING IN SIZE
Here is the idea - like a polyrhythm or like rhythm phasing, the beats are different in each measure - but so also are the measure sizes.
WHAT IS THE MOST UNSYNCHRONIZED RHYTHM YOU CAN POSSIBLY MAKE -- E.G. WHAT IS THE MOST OUT OF TIME THAT TWO DRUMMERS CAN BE IF EACH IS PLAYING A PERFECTLY STEADY BEAT?
This rhythm arises from the question - how out of sync can two musicians possibly be when playing a steady beat? What if you play to be as out of sync as possible?
If you mean by that - that you start together, and both play a steady rhythm, but make sure that none of your beats get close to each other again as long as possible, and be as out of sync as you can right from the start, you might end up with this rhythm.
Here I've set it to emphasize the fourth beat as well in each part to give a feeling of two musicians playing 4/4, as out of sync as they can be.
It's also played on the golden ratio pitch interval - an interval that similarly is in a rather technical mathematical sense, as far away from being "in tune" as possible - but is a rather pleasant musical interval
If you wonder about the pattern of bounces, it's a pattern used by conductors to show 4/4.
The golden ratio is related to the Fibonacci sequence of course (if you are a mathematician) - as you go up the fibonacci sequencee you get closer and closer approximations to the golden ratio pitch interval and golden ratio rhythm.
Like this
This next one has all of the first few Fibonacci rhythms, at Fibonacci pitch intervals with a reverse buzz roll effect.
This next one brings out the connection more, it's the golden ratio rhythm and also pitch interval.
The bouncing numbers help you to see how the beats of the two rhythms nearly coincide when they reach successive Fibonacci numbers 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...So for instance when you get to 21 beats for the blue ball and 34 for the red ball the clicks are close together, and even closer for 34 and 55, etc.Though if you wait long enough you get close together beats eventually, you have to wait far longer than for most rhythm phasing rhythms.
RHYTHMS ONE AFTER ANOTHER - ADDITIVE RHYTHMS
Just to mention these, a huge subject in itself. These are rhythms where you have different rhythmic patterns following each other in a long cycle.
This is a relatively simple one as they go, the rhythm of "blue Rondo a la Turk"
Now let's combine some of these ideas together.
Here is a harmonic polyrhythm, syncopated, and each part plays rhythms accented like the additive rhythms
Accents the 13 as 3+2+3+3+2 and the 5 as 3+2
Pitches: from near to far and left to right: 3/1 8/1 5/1 5/2 6/1 4/1 7/2 1/1
With 13:5 then you would need to do 18 parts playing at once to play all the possibilities - which would be such a dense texture it might be hard to hear what is going on.
In this video then I've done just three parts for the 13 beats to a measure, and three parts for the 5 beats to a measure (plus an extra part to do extra emphasis for one of the 13 beat parts)
These are just some of the very many rhythms and types of rhythm I've been exploring with Bounce Metronome. There are many types of rhythm here I had no idea existed just a few years ago, and it's been a fascinating journey of discovery finding out about them all.
Maybe you'll enjoy them also.
KICKSTARTER FOR BOUNCE METRONOME ON THE MAC
Many musicians have Mac computers of course, also music departments are often Mac based - and I get asked over and over, when will Bounce be available on the Mac. I've been asked that two or three times a month for years now.
So, if you are a Mac musician, here is your chance to make this happen. I've got a kickstarter on right now, just started it, to get this program, Bounce Metronome (and some other programs of mine) running on a Mac.
Bounce Metronome, Tune Smithy, Lissajous 3D... on Intel Mac!
You get an unlock key for all my software for your support (if the project succeeds that is).
The unlock key also works on Linux or Windows and you don't have to be a Mac musician to show your support in this way. Any pledge is appreciated and if you share the kickstarter with others who are interested in such things that's also a great help.
FIND OUT MORE - BOUNCE METRONOME VIDEOS AND PROGRAMS
I have many more videos like this for you, if you want to explore this some more. Take a look at the Robert Inventor youtube channel (well over 600 so far), and the Video Resources section of the Bounce Metronome website.
You can also download Bounce Metronome itself and try these rhythms for yourself (and many more) on Windows or Linux. There's a 30 day test drive with all the features unlocked, enough to have a good explore of them - and you can also renew that test drive if you need to, just ask me for a renewal and get it automatically.
If there are any types of rhythm you would like to see as videos, do let me know. If Bounce can't do it yet, then I'm also always keen to know about new rhythms to add to the wish list for the program.
I've already shown this, in another recent article, but think it bears repeating.
Here is the golden ratio 'cello tune, one of the tunes that come with Tune Smithy. The rhythm uses the Fibonacci gamelan patterns we started with - but with the beats distributed around over many parts - a technique known as hocketting where one part passes its tune or rhythm to another part in a sequence. But it does other transformations as well on top of that - beats stretched and compressed together over and above the Fibonacci two beat sizes.
The video here is a Mandelbulb fractal by Torsten Stier.
More like this: playlist of many of these fractal tunes + fractal videos


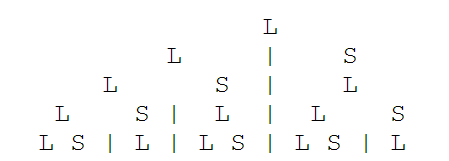





Comments