What ties together Lissajous knots, the harmonic polyrhythms of Theremin's rhythmicon, and a way of adding sounds to Pendulum waves? And do they have healing properties? And what is the musical maths of sloth canon number sequences?
One of my first posts here was on the Music And Mathematics Of Fractal-Like Sloth Canon Number Sequences. But since then I've been posting mainly about Mars and space colonization. Today though, I just launched a kickstarter to help get my Windows programs running on the Mac, and thought it was a nice opportunity to talk again about some of these ideas on the interface between music and maths, especially focusing on the harmonic polyrhythms, which tie together Lissajous knots, Theremin's rhythmicon and the pendulum waves.
HARMONIC POLYRHYTHMS
This is an idea explored by Henry Cowell, in a famous book called New Musical Resources, and he commissioned the Russian inventor Theremin - the same chap who made that instrument that you play just by waving your hands in the air around it - to make the rhythmicon, long before personal computers in the 1960s.
It lets you hold down any notes in the harmonic series and each note plays at a different tempo depending on its frequency. They interact to make complex and interesting rhythms, "polyrhythms" in fact - a kind of mash up of independent rhythms played simultaneously.
Rhythmicon demonstration
Bounce Metronome has its own version of Theremin's rhythmicon which you can try out for yourself. It doesn't emulate everything, doesn't have that rather wonderful drop in pitch as the machine slows down :).
Many cultures have polyrhythms. You get them in Western music also - not so much as elsewhere - but 3:4 and 3:2 is common. Chopin makes a lot of use of polyrhythms, including sometimes playing a row of say 22 notes over 12, ( Chopin's Nocturne op. 9 no. 1 in B flat minor) though meant to be played with rubato, i.e. not in strict tempo.
Some composers such as Ligetti made a lot of use of them. He was influenced by the Efe people - the "pygmies" and other polyrhythms in Subsaharan Africa.
Efe People's Rhythms and Polyrhythms
It's a playlist of an hour and a half of Pygmie music with lots nice rhythms including many polyrhythms - they are noted for them. The tuning of the music is also interesting for those interested in microtonal music.
See Efe People and Efe People of the Ituri forest for more about the people who make this music
Polyrhythms are also used a lot in Indian music.
LISSAJOUS PATTERNS IN 3D
You may well know the Lissajous patterns you get in 2D. Plot two frequencies against each other, one horizontally, and one vertically, and you get a pattern like this
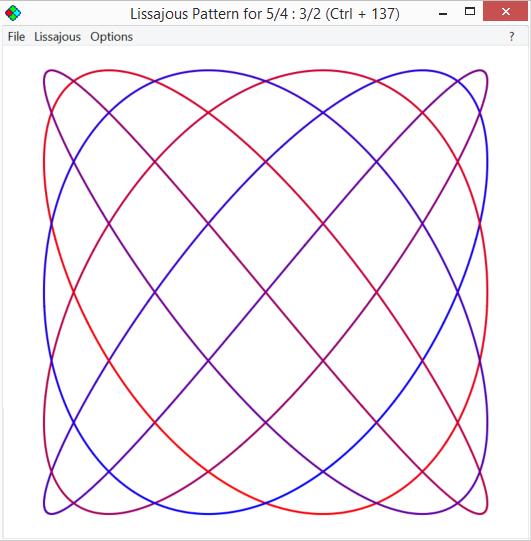
The idea is simple. Think of a point that vibrates five times from left to right for every time it vibrates three times back and forth horizontally. Then this is the path it would trace out on a sheet of paper.
You can make the Lisssajous patterns using an oscilloscope. Originally they were made using mirrors attached to tuning forks.
Here is a later version, using two mirrors attached to vibrating wires at right angles.
Which makes the Lissajous pattern like this:
To find out more with wonderful pictures of these ancient Lissajous mechanical devices, in this article Lissajous Figures by Thomas Greenslade
For a while, Lissajous patterns were used for fine calibration of new tuning forks. Here are some tuning forks with mirrors attached from the late nineteenth century.
Nowadays you can do it much more easily with lasers, like this
Lissajous Curves with Tuning Forks
And here is an example with the two tuning forks in frequency ratio of 8 9
But what if you add a third wave? If you want to represent musical harmonies with Lissajous figures that's going to happen often.
That's a question I had to tackle with my "Tune Smithy Lambdoma".
This is a program to show an arrangement of musical pitches used for music therapy, attributed to Pythagoras. What he actually taught is a matter of mystery, as no writings survive (for an overview of modern scholarship about what he actually taught, see Pythagoras (Stanford University) ). All we have are his sayings, and the accounts of later scholars.
In the case of the Lambdoma, then the basis of this attribution is a commentary by the Greek Iamblichus regarding the Lesser Arithmetic of Nicomachus, which was studied by German scholars of the nineteenth and twentieth centuries, starting with the dedicated amateur nineteenth century scholar Albert von Thimus, who were first to introduce the Lambdoma matrix into modern times. For a detailed account of this possible connection of the Lambdoma with the teachings of Pythagoras, see "Musica Universalis: from the Lambdoma of Pythagoras to the tonality diamond of Harry Partch" by Scott Eggert.

Again mathematically it's very simple. The numbers show the ratios of the frequency of that square to the 1/1, which you can set to any arbitrary pitch, say 440 Hz or middle C, or 256 Hz or whatever.
Then the diagonal row running up from the bottom corner to middle right is a musical harmonic (or overtone) series 1/1, 2/1, 3/1, ... just multiples of the original frequency.
(If you are a mathematician, well it's related to, but not the same as the harmonic series of mathematicians which is the sum of all those terms).
The other diagonal row is a subharmonic (or undertone) series 1/1, 1/2, 1/3, 1/4, ...
It's easy to see, that all the other rows in both directions are the same sequence of pitches, just shifted up or down. For instance the second row diagonally up to right is the same as the first row but with all the numbers divided by 2, so shifted down an octave.
So, the end result of this simple process of putting all the ratios of the numbers 1 to 8 in a lattice like this is an interlocking array of harmonic series going up to the right, and subharmonic series going up to the left.
Note, this Pythagorean Lambdoma tuning shouldn't be confused with the Pythagorean twelve tone tuning of Medieval Music and it's generalizations, a different tuning system, based only on multiples of 3 and 2.
INTERLOCKING MAJOR AND MINOR CHORDS PATTERNS
It turns out that the purest major chord you can make uses the fourth, fifth and sixth harmonics 4/1, 5/1, 6/1. Similarly you find the purest minor chord as 1/4, 1/5, 1/6.
So the arrangement of pitches here is a sort of criss-crossing pattern of major and minor chords - except, that it also extends beyond the harmonies of western music to encompass the seventh harmonic, here as the 7/1 and the 1/7 and its multiples 7/2, 7/3 etc and 2/7, 3/7 etc.
The harmonies of Western European music are restricted to approximations of intervals made up of ratios of multiples of the primes 2, 3, and 5 - and in the middle ages was even more restricted, to just the primes 2 and 3 - but music of other cultures explores the higher harmonics. You can think of them like a kind of extension of our major and minor to higher harmonics in the harmonic series.
Barbara Hero took this idea from Greek mathematics and added details to do with colours, then the Lissajous patterns, and then recently, made this connection with harmonic polyrhythms like the rhythmicon. I just wrote the software to help put her ideas into practice in this case.
This pattern is closely related to Harry Partch's tonality diamond, but not exactly the same.
Harry Partch, remarkable mainly self educated genius, one time hobo (during the great depression), instrument maker, and pioneer of much of modern microtonal music theory.
In the tonality diamond, you ignore octave repeats, reduce everything into the octave and arrange in order of increasing size for convenience of musical playing.
For more about the connections between the Lambdoma and the tonality diamond see Scott Eggert's article again.
LISSAJOUS PATTERNS FOR TRIADS - AND LISSAJOUS KNOTS
It was easy to draw Lissajous patterns for Barbara Hero's ideas, for two note chords, but for a three note chord you end up with something like this
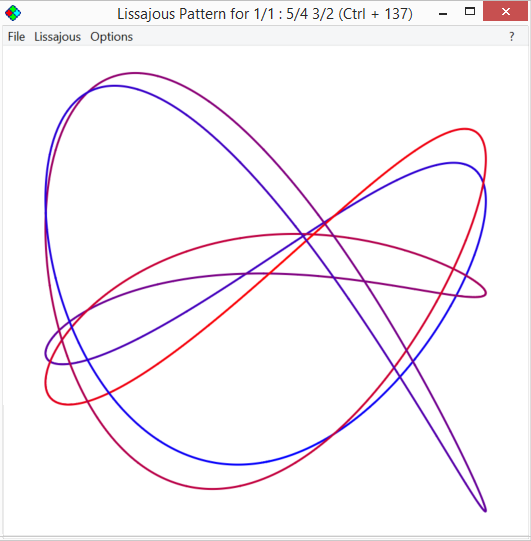
That's with two of the waves one way, and one the other way.
You can also try the idea of putting them in three different directions, equally spaced and you get
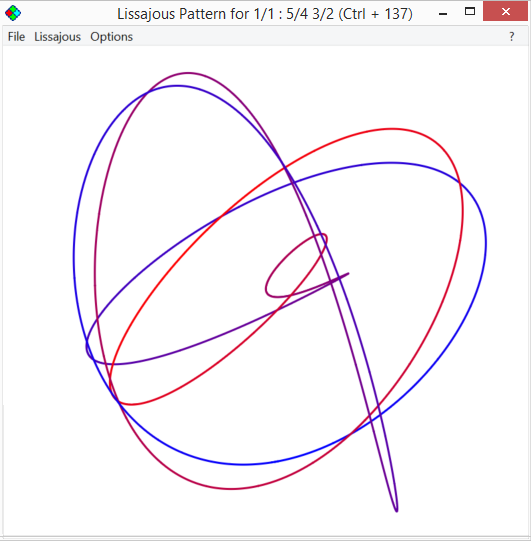
They are nice enough patterns for sure, but don't really show the connection between the three waves of the triad so clearly.
So anyway the composer Charles Lucy of Lucy tuned lullabies suggested, why not put the third axis into 3D? I don't know why I didn't think of that. Did that and here is the result, for the same example, a major chord. This video clip also plays the notes of the chord
Frequencies in ratios 1/1 : 3/2 : 5/4, Lissajous 3D, Polyrhythms with tempi in same relationship
It gives a far clearer visual representation of the relationships between the three frequencies.
Later, I found out that this is an old, known idea, called "Lissajous knots" by mathematicians. I actually studied a bit of knot theory, in my own time for interest, but missed out on this.
Knot theory is about the study of tangled closed loops in mathematics. It's a bit different from the everyday idea of a knot which relies on friction to join ropes to each other and to other things. A mathematical knot means a tangled loop of string with no ends to it., which can't be untangled except by cutting it.
Mathematicians then say that two knots are "the same" if you can make one into the other by any amount of stretching and disentangling, or untying, but with no cutting permitted. It's a tricky subject, with surprising, unexpected connections with particle physics, specifically a three dimensional topological quantum field theory called the Chern–Simons theory through the Jones polynomial which is used nowadays to resolve many questions in knot theory.
If you make the third frequency quite high, you get rather fine 3D representations of many common knots like this
Here is the same knot in Lissajous 3D

821 knot
Maths details for anyone who wants to input Lissajous knots into the Lissajous 3D program: the Lissajous knots are described using five parameters nx, ny, nz and ϕx, ϕy.
To display in Lissajous 3D, you enter the nx, ny, nz as across, up and in, in the shape window. You set the "across" phase shift to 90 + 180*ϕx / π . the "Up" phase shift to 90 + 180*ϕy/π and the "In" phase shift to -90 degrees
In this case, it's 3, 4, 7 for across, up and in, and then phase shifts 90 + 180*0.1/PI across, 90 + 180*0.7/PI up, and 270 in. You can just enter those as formulae as Lissajous 3D recognizes formulae input to any of its text fields.
I'll add a window to make it easy to enter these figures for lissajous knots, no need to use these formulae, along with a droplist of examples in next version of Lissajous 3D.
Many simple knots can't be made as Lissajous patterns, such as for instance the trefoil knot, you can prove that no Lissajous pattern in 3D can make this. In other words, no matter how you stretch and pull this shape around, so long as you are not permitted to cut it and rejoin the pieces, it will never make a Lissajous pattern.
Trefoil knot, example of a mathematical knot that can't be made as a Lissajous pattern
But there are infinitely many Lissajous knots you can make, of course and they are interesting because of their high degree of symmetry.
LAMBDOMA AND MUSIC THERAPY
The Lambdoma arrangement of pitches and the Lissajous patterns are used in music therapy by various music therapists in the States and in Taiwan. They have various ideas about why they work and how to use them.
As someone with a scientific background, then I have no idea what some of them mean by the things they say. For instance I simply can't attach any meaning to the idea that particular pitches resonate with atoms in your body, or that particular frequencies help with DNA repair of various parts of the body (I may not be describing their ideas accurately given I don't understand any of it but - that sort of thing).
The wavelength of a 256 Hz tone for instance is 331.2/256 or 1.29 meters (that's at 0°C) - what can that possibly do to a DNA molecule of width about 2.5 nanometers (nanometer is a billionth of a meter)?
But what if they are onto something? If not presented in a way that's easy to fit within present day science. Perhaps it is more like a scientific metaphor or poetry at present?
I'm prepared to keep an open mind, there are many things we don't understand. As Isaac Newton is reported to have said
I do not know what I may appear to the world, but to myself I seem to have been only like a boy playing on the sea-shore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me.
Tung Ping Chau, Hong Kong
I think, in many ways, we are like that still, given the vastness of the universe, so little we really understand.
We haven't yet sent anything as far as the nearest star, and our solar system itself is hardly explored at all close up. Everything else is inference from patterns of light, fast moving energetic particles, and radio waves and such like, detected from the distance by our telescopes. Also limited in time, only been doing science for a few centuries, and written records go back only thousands of years, a millionth of the age of the universe. Limited in energy, we can use only a tiny fraction of the solar energy that falls on the Earth, never mind the amount of energy that is emitted by the sun.
Also, we haven't done any scientific experiments that last for as long as two centuries
The Oxford electrical bell, which has been ringing continuously since 1840, possibly for 15 years longer, (with occasional interruptions when humidity is high), needs no winding up, often cited as the longest running scientific experiment.
If we need to do an experiment on a longer timescale than that, for instance, to leave an ocean full of organics for a hundred million years to study how evolution gets to the primitive cells from amino acids, we have no way of doing it. We just have to hope that nature has done the experiment for us. We are also limited in the range of extremely short time scales and high precision in space, such as the Plank scale, as this requires vast amounts of energy.
And our universe is so young also, compared for instance with the trillions of years lifetimes of an orange or red dwarf star, with the largest stars shining brightly still and many young stars newly forming all the time. How can we imagine we really have a clear understanding of everything that we can study in our science? It's no surprise that along with all our knowledge, we also have countless mysteries we don't really understand.
Indeed, a rather whmisical but fun thought. If we meet ETs, what if they don't have scientists, like us, and in their place have artists, poets, musicians, and therapists who think in similar ways. perhaps talk about harmonies resonating with atoms in their bodies and so forth? And perhaps build spaceships out of music or poetry? And warp the universe with thought and ideas rather than technology? After all in some ways, according to some ways of looking at things, thoughts are more fundamental than our technology philosophically speaking.
You get a few ideas like that explored in science fiction sometimes. I don't know how likely it is, that we might meet ETs like that, but if it does happen, we might find each other mutually pretty incomprehensible to start with.
I wouldn't want to say at all that we ditch science of course. When it is at its best, it is just rigorous thinking, and making sure you don't fool yourself with wishes and delusions. If it was possible to navigate the galaxy with spaceships made of poetry and music, you could look at how that works as a scientist also. It's not really at all limited to conventional ideas of what science is about.
Einstein's quote, similar to the Newton and also often quoted brings this out, the value of science and rigorous thinking in all its forms.
"One thing I have learned in a long life: that all our science, measured against reality, is primitive and childlike -- and yet it is the most precious thing we have."
I wonder sometimes though if we might need new methods of rigorous thinking that, for some reason, we simply haven't invented yet. Science does seem rather limited when it comes to holistic things, such as music therapy indeed. You can't really do a double blind experiment for instance, it's not like pills where the control is a pill that looks the same but hasn't got the active ingredient.
Anyway, whether their explanations do have some meaning I can't grasp, I can well understand that the harmonies of the Lambdoma matrix and the Lissajous patterns could have healing properties - just because of the healing effect of listening to harmonious sounds and watching gentle smooth curves as you play on the keyboard.
You can give it a go yourself with the Tune Smithy Lambdoma and see if you think it does have a healing influence.
Also you could have a listen to this video as a kind of intro to the many ideas around about musical pitches with healing properties (nothing to do with Barbara Hero) demonstrating some pure ratio intervals played.
Do you feel healing effects of these musical intervals when they are played? Many of those commenting on the video do.
If you do think that things like playing musical tones, for instance, may have profound healing properties on the body - then as scientists, or scientific by inclination, is there any way we could look into it?
Can we hope to find out in any rigorous way if these musical tones in harmonic relations do help to heal the body (and mind also especially mental trauma)? And if they do, can we maybe make new scientific discoveries that can be of value to the music therapists that work with them? Or is it just not amenable to that sort of study?
What are your thoughts on all this - do say in the comments below.
PENDULUM WAVES
I wonder if you've seen these?













Comments