So, you think you know what a planet looks like? A sphere, perhaps flattened at the poles? But if you've been following recent discoveries of dwarf planets, you may know that rapidly spinning dwarf planets like Haumea typically are rugby ball shaped (triaxial spheroids), rather surprisingly perhaps. So, what other shapes can a planet have? Theory, and experiment with droplets in simulated zero g suggest several exotic possibilities.
In Hal Clement's classic hard science fiction novel Mission of Gravity his explorers discover a rapidly spinning planet, and naturally enough he imagines it as flattened at the poles, in the same way as the Earth but more so
He imagined it as an oblate spheroid
When he wrote that nobody had ever discovered a rapidly spinning planet. But now we have found very rapidly spinning dwarf planets in the outer reaches of the solar system, and it turns out, that they look like this (at least the ones found so far):
Haumea: Rugby Ball Planet - artist's impression
And here is an artist's impression of Haumea spinning, with its red spot.
Another example 20000 Varuna - artist's impression
They may look similar to Hal Clemens planet, but are actually a little different. These are triaxial ellipsoids
Ellipsoid
They rotate around their minor axis, the shortest of the three axes.
It turns out that both these shapes are right, because there are two possible solutions, as the spin rate increases. You can get an oblate spheroid, or a triaxial ellipsoid - the solution "bifurcates". But the triaxial ellipsoid is the most stable of the two as Jacobi dramatically predicted, over a century ago, in his paper published in 1834 - overturning the previous prediction that rapidly spinning planets could only be oblate spheroids.

The mathematician Jacobi, who predicted that rapidly spinning planets could take the form of triaxial ellipsoids in 1834
For more about the history of mathematical equilibrium solutions for rapidly spinning planets, see this Figures of Equilibrium - Historical Account - by Chandrasekhar.
Subrahmanyan Chandrasekhar, author of Figures of Equilibrium - Historical Account - best known for his work on collapse of stars to black holes and the Chandrasekhar limit.
In practice, this triaxial ellipsoid is the shape that the rapidly spinning dwarf planets take, preferentially.
Now if that seems bizarre, it's not the most unusual planet shape possible.
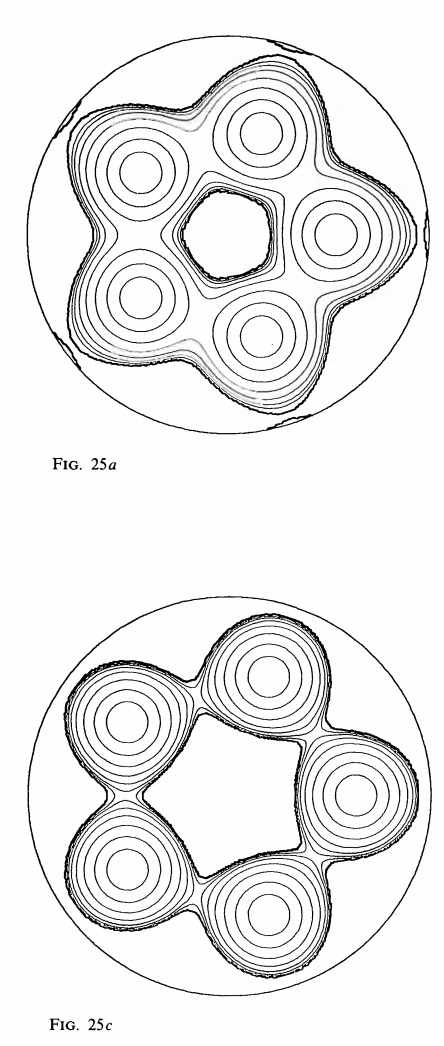
Planets can actually be triangular, or square, or even pentagonal in shape in theory. And in principle they can also be donut shaped too, with a hole in the middle - a stable configuration though one that is easily disturbed so there probably aren't that many donut shaped planets in the universe :).
For that to happen they have to be spinning so fast they are on the verge of breaking apart.
There are cool videos of triangular and square droplets in simulated zero g here.
LiveLeak.com - Spinning water droplets behave like black holes
Here the droplets are held together by surface tension. But apparently theoretically droplets held together by surface tension in zero g have the same shapes as droplets that form from a wide range of processes including a planet or star held together by gravity. So this is experimental work that also confirms theoretical predictions for possible shapes of planets too.
So these are also possible shapes for rapidly rotating planets. Paper here: Nonaxisymmetric Shapes of a Magnetically Levitated and Spinning Water Droplet
Then as it spins faster, it can turn into two spheres joined together. This is the scenario of a binary planet.
GRAVITATIONALLY LOCKED BINARY PLANET
Normally planets can't get too close to each other, or they will tear each other apart through tidal forces. But if the two planets are gravitationally locked to each other, in the same way as Pluto and Charon, then tidal effects no longer matter.
Binary planets like that are just permanently distorted, and so can be as close together as you like. You could in principle even have an Earth sized planet almost touching our Earth - with a shared atmosphere and ocean, and the Earth would be in no risk of tidal disruption. They can even join together in an "overcontact binary" in principle.
Indeed recently some scientists suggested that we may find habitable double worlds like this as we continue to search for exoplanets.
This idea is explored fictionally in Robert Forward's "Rocheworld". In his case it is an "overcontact binary" - well at least the atmosphere is shared between the two planets, and sometimes the ocean
We haven't found any Rocheworld planets yet, but there are many contact binary asteroids. These are too small to be rounded under their own gravity - still, they are approximately the shape of an overcontact binary, and are probably "loose rubble piles" mainly held together by gravitational effects like a contact binary planet.
This is 216 Kleopatra
And comets also, this is 67P/ChuryumovGerasimenko which is also approximately the shape of an overcontact binary
And we now know of a contact binary moon, at least it seems so, Pluto's tiny moon Kerberos.

Also many contact binary stars are known, again including "overcontact binaries" also like these asteroids and comets, so close together that their atmospheres overlap - the first discovered W Ursae Majoris.
figure from: Chapter 19-7 and for another image see also Contact Binaries
As it spins even faster then in theory anyway, a planet or star can turn into three or even four spheres joined together to make an "overcontact ternary" or "overcontact quarternary" planet or star, or you could have a donut shaped planet too, though so far we haven't found anything like this:
See Viewpoint: The many shapes of spinning drops
This is an animation someone did of the last possibility the "hoopworld"
But thin hoops like this are unstable and easily break up into droplets.
Thicker hoops like this visualization from io9 though can be stable.
I shouldn't think there are many of these in our universe :). Needs very special conditions to form. But - not impossible apparently.
Here is a youtube video of a Moon of a donut Earth:
You can also get donut shaped solutions for end state of a collapsing gas cloud, which are stable, in principle. So, you could have a huge toroidal planet with a young star at the center, as the author suggests in this paper : General Relativisitic Sturcture of Star Toroidal Systems (1992).
Anders Sandberg's fun article explores many aspects of life on a donut shaped planet - and the orbits of satellites and moons around such a planet.
What would the Earth be like if it was the shape of a donut?
There are many other possibilities not shown in that diagram, including the rounded triangles, squares and pentagons, cross shaped, and also three, four or five bodies in contact with each other in a circle with hole in the middle, like this.
TIDALLY STRETCHED PLANETS
This is another way that planets may vary in shape from the usual round or oblate spheroid. Gravitationally locked tidally stretched planets can be triaxial ellipsoids as well, with the long axis towards their sun.
Again we don't know of any planets like this yet. But we do have moons. They are too small to be in gravitational stasis, but the innermost moons of Jupiter do seem seriously tidally squished - or at least - with their long axis aligned towards Jupiter - as you can see from these photographs of them taken by Galileo:
In this photograph then Jupiter is to the right. So they are stretched out towards Jupiter. Catalog Page for PIA01624
Here are more images of the largest of these moons, Amalthea

And in colour, an image taken by Voyager (it is very red, probably because of sulfur from Io)
Amalthea (moon)
In a recent paper, last year stretched-out solid exoplanets (the paper itself with the mathematical details is here: The observational effects and signatures of tidally distorted solid exoplanets) the authors suggest we may soon discover ellipsoidal rocky planets tidally locked to a red dwarf star. They also suggest that some of these may be in the habitable zone. They describe their light curves in detail and suggest ways we might be able to detect them.
Red dwarf stars are much smaller and cooler than our sun. So planets have to "huddle" close to the star to keep warm. The habitable zone is so close to the star that an Earth like planet orbiting a red dwarf star would be tidally locked, and these authors suggest, also ellipsoidal in shape. They could be squished out towards their sun, by as much as 3 : 2.
WHAT WILL WE FIND NEXT AS WE EXPLORE NEW DWARF PLANETS AND EXOPLANETS
Surely we will find more rugby shaped dwarf planets in our solar system and eventually find rugby ball shaped exoplanets too, either tidally squished or rapidly spinning.
Will we find Roche world type overcontact binary dwarf planets in our solar system (I mean in gravitational equilibrium rather than the common over contact binary type smaller asteroids or comets)? Or Roche world exoplanets? Or the more exotic overcontact ternary, quarternary or donut shaped planets - or the theoretically possible toroidal young stars? Or even the rounded triangular, square or pentagonal stars or planets you can get at some resonant spin rates for droplets in the zero gravity analogue water drop experiments?
Well I suppose only time will tell. It's fun to speculate anyway. What do you think?
This originated as my answer to the Quora question "Why are planets round"
See also: Can A Planet's Moon Be As Bright As Its Sun? and Can Moons Have Moonlets? Or Rings? Moonlets Of Pluto's Moons?
SIMPLE QUESTIONS - SURPRISING ANSWERS
This is also one of the answers in my new kindle book: Simple Questions - Surprising answers - In Astronomy
You can read it on any device, not just a kindle, and also, read it with the kindle cloud reader in your web browser.
ONLINE POSTS
You might like my other posts on Quora

Robert Walker's posts - on Quora
And here on Science20

Robert Walker's posts on Science20
KINDLE BOOKSHELF ON MY AUTHOR'S PAGE
And I have many other booklets on my kindle bookshelf
 My kindle books author's page on amazon
My kindle books author's page on amazon







Comments