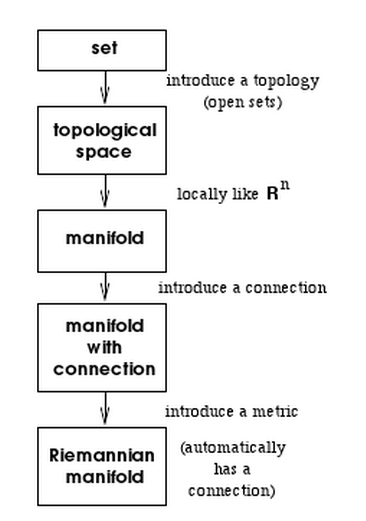
RETRACTED: It's a bug of general relativity

[Retracted: In this blog I hope to get to a well known issue in general relativity, namely that gravitational energy needs to be defined for a spacetime volume instead of at a point.] The [new] goal is to sketch the Riemann curvature tensor...

There are limitations to what one can do in a blog. The flowchart is from Sean Carroll's lecture notes that I highly recommend. In this blog, I will presume I am working with a Riemannian manifold, the final step of the geometry construction. A Riemannian manifold allows one to do differential calculus even in curved spacetime.

There still are choices to be made. One of the key choices is the sort of connection to use with the manifold, in step 3 of the flow. Should the connection involve a metric? Should the connection account for torsion? Since the blog concerns general relativity, the choices made in that theory are for a connection that is metric compatible and torsion-free. In practice that means one works with the Christoffel symbol of the second kind (that almost sound like a movie title). The Christoffel employs three derivatives of a metric:

$\Gamma_{\gamma \alpha \beta} = \frac{1}{2} \left( \frac{\partial g_{\gamma \alpha}}{\partial x^{\beta}} + \frac{\partial g_{\gamma \beta}}{\partial x^{\alpha}} - \frac{\partial g_{\alpha \beta}}{\partial x^{\gamma}} \right)$

The Christoffel symbol is not a tensor even though those look like tensor indices. It is also "flat" in a technical sense (discussed by Carroll at the bottom of page 73, partly because moving a vector with a given Christoffel keeps it pointed in the same direction).

Where does one use Christoffel symbols? Start with a 4-potential. Then take its 4-derivative. Unfortunately the result is not a second rank tensor. The reason is that spacetime may be curved. When that happens, the changes in the potential will remain silent to the changes in the curved spacetime. A covariant derivative can account for both changes in the potential and in spacetime:

$\nabla_{\mu} A_{\nu} = \partial_{\mu} A_{\nu} - \Gamma^{\sigma}_{\;\mu \nu}A_{\sigma}$

The covariant derivative does transform like a tensor. One term keeps track of changes in the potential, the other will add up all changes due to curvature.

In EM, the field strength tensor uses this covariant derivative and its antisymmetric twin:

$F_{\mu \nu} = \nabla_{\mu} A_{\nu} - \nabla_{\nu} A_{\mu}$

The Christoffel symbol is symmetric, so it will drop out of this calculation. In EM, one needs to supply a metric as part of the background mathematical structure. Whenever I read about the background structure, I like to re-read a post from John Baez on the subject.

General relativity on the other hand provides a means for determining what metric applies based on the physical conditions. The tool for this task is known as the Riemann curvature tensor. Consider a 4-vector in spacetime. Move it around a bit, but eventually bring it back to its starting place. Will the 4-vector remain the same? It will if spacetime is flat. If spacetime is curved, then the 4-vector will point in a different direction.

The Riemann curvature tensor quantifies the difference between the starting and ending vectors caused by the curvature of spacetime. This is done by looking at the difference between two paths:

$R^{\rho}_{\;\sigma \mu \nu}= \partial_{\mu} \Gamma^{\rho}_{\;\nu \sigma} - \partial_{\nu} \Gamma^{\rho}_{\;\mu \sigma} + \Gamma^{\rho}_{\;\mu \lambda} \Gamma^{\lambda}_{\;\nu \sigma} - \Gamma^{\rho}_{\;\nu \lambda} \Gamma^{\lambda}_{\;\mu \sigma}$

This complex creature does transform like a tensor even though the Christoffel symbols do not. Recall that the Christoffel has first order derivatives of the metric, so the curvature tensor has second order derivatives of the metric. Solutions to second order differential equations of the metric can be used to define a dynamic metric (not completely however).

A reductionist points to two critical properties: as the name implies, the Riemann curvature tensor transforms like a tensor and this tensor contains within it second order derivatives of the metric. This is the central tool for general relativity. The vacuum field equations are the difference between the Ricci tensor, a contraction of the Riemann curvature tensor, and the Ricci scalar, a contraction of the Ricci tensor:

$R_{\mu \nu} - \frac{1}{2} g_{\mu \nu} R = 0$

The reason one needs both the Ricci tensor and scalar is to conserve energy via the Bianchi identities. Since these tensors are contractions of the Riemann curvature tensor, they both are tensors that contain second order derivatives of the metric.

Riemann Normal Coordinates

One picks coordinates to make things simple. The Riemann normal coordinates are nice in the way they ensure the partial derivatives of a metric vanish at a particular point p. At that point p, all the Christoffel symbols are zero since the Christoffel is a contraction of three partial derivatives of a metric. It is vital to note the disappearing act only happens at the point p, not its closest neighbor, call it p'. Curved spacetime remains curved in Riemann normal coordinates. The Riemann curvature tensor cannot be made zero by the choice of Riemann normal coordinates since the curvature tensor accounts for changes between points p and p'. [Retracted: This underscores the need to look over a volume of spacetime when thinking about general relativity].

In an electric field, every point on the manifold will have a field strength, and from that, a corresponding energy (ignoring issues that arise from singularities). [Retracted: In contrast, it is more difficult to know what one means for a point in spacetime if curvature necessarily involves a comparison between two points. Certainly there are limit processes, but that becomes a concern in light of the Riemann normal coordinates since one cannot eliminate spacetime curvature by a choice of coordinates.]

[Retracted: Some consider this issue a feature of general relativity, the need to work with volumes of spacetime to define the energy of a gravitational field. This is a fundamental way the fundamental force of gravity is different from the other three forces of Nature that can be defined point-wise. ]

The only way to get a paying job in gravity theory research is to presume the Riemann curvature tensor is part of the way Nature works in practice. Even folks working out in eleven dimensions justify their funding by pointing to the Einstein field equations sitting in their high dimensional stew. Loop quantum gravity work presumes the Einstein field equations are a point of departure for constructing spin foams at the Planck scale.

Before I present my own evolving position, let me remind the reader of a few things. This is just a blog. My views are my views. I am not asking you to follow. I write to clarify my own perspective. Should you disagree, please remain polite so I don't have to deal with violations of the golden rule.

[Moderation aside: I used to participate in the moderated newsgroup sci.physics.research. In one points, I described the problem that has been around since 1930, getting general relativity to play nicely with quantum mechanics. The current efforts try to bend one toward the other with fancy math, taking care to break neither. I suggested a simpler idea: what if general relativity was wrong? There is a long tradition to directly confronting old, widely accepted theories in physics. GR beat Newtonian gravity by experimental tests. Alas, the post was deemed overly speculative.]

[Retracted: If fields must be well-defined for every point in a spacetime manifold, then the Riemann curvature tensor represents a bug.] There [may] be another expression that transforms like a tensor yet contains within its bounds a second order derivative of a metric tensor. It should be obvious, but apparently isn't, that any second order covariant derivative contains second order derivatives of a metric tensor. The first covariant derivative has a metric compatible connection which contains first order derivatives of a metric. Take a derivative of that, and one necessarily has a second order derivative of a metric that at least stands a chance of characterizing a dynamic metric.

[Discussing below, so of questionable value: The Lagrangian of general relativity now strikes me as a rigged game. We need second order derivatives of a metric, so start with the Ricci scalar which contains a second order derivative in its heart. Vary that with respect to a metric, and voila, the field equations still contain second order derivatives of the metric. In EM, the fields are first order derivatives of the potential. The field equations are second order derivatives of the potential. That is how the game should be played.]

It is vital to look at general relativity with the eyes wide open. [Clarification: I am biased. As someone trying to make an alternative proposal for gravity, I am hoping to find a subtle issue that indicates a flaw. Yet I have said for a few years that the more one learns about GR, the more impressive are its accomplishments]. How good is the data? An honest answer is needed. Here is the Schwarzschild solution in isotropic coordinates, the sort of coordinates that will be used in experimental tests:

$d \tau^2 = \left( \frac{1 - \frac{G M}{2 c^2 R}}{1 + \frac{G M}{2 c^2 R}}\right)^2 d t^2 - \left( 1 + \frac{G M}{2c^2 R}\right)^4 \left( d R^2 + R^2 d \theta^2 + R^2 \sin^2 \theta ~d \phi^2\right)/c^2$

I always have to look this form up. The value of GM/c²R is small, even for the Sun at its surface (2.12 x 10^-6).

$g_{tt} =1 - 2 \frac{G M}{c^2 R} + 2 \left( \frac{G M}{c^2 R} \right)^2 - \frac{3}{2} \left( \frac{G M}{c^2 R} \right)^3 + \left( \frac{G M}{c^2 R} \right)^4 + O(5)$

wolframalpha

$g_{RR}=1+ 2 \frac{G M}{c^2 R} + \frac{3}{2} \left( \frac{G M}{c^2 R} \right)^2 + \frac{1}{2} \left( \frac{G M}{c^2 R} \right)^3 + \frac{1}{16} \left( \frac{G M}{c^2 R} \right)^4 + O(5)$

wolframalpha

In physics as in beauty contests, the prettiest equations always win. The exponential metric is prettier:

$d \tau^2 = e^{-2 \frac{G M}{c^2 R}} d t^2 - e^{2 \frac{G M}{c^2 R}} d R^2/c^2 - R^2/c^2 (d \theta^2 + \sin^2 \theta d \phi^2)$

I never have to look this one up. The Taylor series is better looking too, particularly the way the terms for changes in time are identical to those for changes in space forever.

$g_{tt}=1-2 \frac{G M}{c^2 R}+2\left( \frac{G M}{c^2 R} \right)^2- \frac{4}{3}\left( \frac{G M}{c^2 R} \right)^3 +\frac{2}{3} \left( \frac{G M}{c^2 R} \right)^4+O(5)$

wolframalpha

$g_{RR}=1+2 \frac{G M}{c^2 R}+2\left( \frac{G M}{c^2 R} \right)^2+\frac{4}{3}\left( \frac{G M}{c^2 R} \right)^3 +\frac{2}{3} \left( \frac{G M}{c^2 R} \right)^4+O(5)$

wolframalpha

It should be simple to distinguish between these two: go do the measurement, and the real one will win. Surely this has been done, right? The answer is no, it has not been done. Recall how small GM/c²R is for the Sun. The classical tests of general relativity have measured these terms of the Taylor series and no others:

$\\ g_{tt} = 1-2 \frac{G M}{c^2 R}+2 \left( \frac{G M}{c^2 R} \right)^2 + O(3)\\ \\ g_{RR} = 1+2 \frac{G M}{c^2 R} + O(2)$

Both metrics are the same. Why no more? This was hard enough to do in 1919. There are some technical questions over whether the data did support the conclusion reached at the time. Radio wave astronomy made it possible to repeat the light bending tests at any time of year. The current resolution is at 100 microarcseconds, 10,000 times better than in Einstein's time, but a factor of 100 less than needed to tell the difference between these two metrics.

Formulating a new proposal is not an all or nothing game. It is an all or -500 game. One person did not wish me to write this post, so he offered to pay for mental health services for me instead. Given the high costs of such professionals, I did not take him seriously and deleted his request (he did not log in so i was unable to haggle over the costs). Let me talk about my hypercomplex gravity failure. What I wanted were two fields that were like those in EM, but different. I placed a few conjugate operators in there so the fields were different. There were multiple flaws leading to the retraction.

The tension in my research on gravity is how to make it different from EM, but not too different. The hypercomplex gravity proposal was too different. Now I am feeling a tug the other direction, to someday (not today) come up with an idea that is more like EM, yet all about geometry. In EM, I see three levels:

The potential:
$A_{\mu}$

The fields:
$F_{\mu \nu}=\nabla_{\mu} A_{\nu} - \nabla_{\nu} A_{\mu}$

The field equations:
$\\ \nabla_{\nu} F_{\mu \nu} = J_{mu}\\ \\ \nabla_{\gamma} F_{\mu \nu} + \nabla_{\nu} F_{\gamma \mu} + \nabla_{\mu} F_{\nu \gamma} = 0$

One generates the source field equations by varying the action with respect to the potential.

In general relativity, everything is different. There is no potential. In EM, the action arises from a contraction of the field strength tensor which is a derivative of a potential. In GR, it is like they know they need to work with the Riemann curvature somehow, and the Ricci scalar does the trick (it certainly does). Because it is as pure geometry as anything can be, it cannot be linked to the other three forces of Nature. At least not after generations of work by theoretical physicists.

Because the field strength tensor of EM is antisymmetric, it cannot speak about metric geometry. Perhaps a proposal that starts with the fields of EM but goes smaller in some technical fashion, the field equations that result can only speak of geometry. The fields are the same, but the field equations are different. It is something to dream about.

Doug

Snarky puzzle: Calculate the Christoffel symbol for the exponential metric.

Next Monday/Tuesday: GR vs QFT - DiscussNote: I will set up the question, but not provide my own answer in the blog, saving that for the comments which you can skip ;-)

Related articles

Comments

Know Science And Want To Write?

Donate or Buy SWAG