In this blog, I will review my thoughts on the action of general relativity, how it is used for the field equations and equations of motion. There is much to consider, so perhaps this will create a means for discussing this deep subject.
The Action
It was Hilbert who wrote down the action of general relativity based on discussions with Einstein.
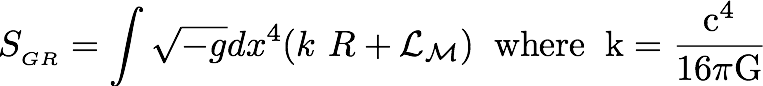
While this happens to be the first action published for general relativity, there are other actions available. In particular, there is the Palatini action which allows one to include non-integral spin matter fields. This is the kind of little factoid I worry about. The ultimate theory for gravity must have a way to handle fermions. Why should the Hilbert action be discussed if it has this seemingly fatal flaw? All fermions have mass, so how are the technical cognescenti dealing with this issue? The more I think about it, the more upset I get. I would have retracted the action if it was mine because one fatal flaw is one too many :-) I will proceed anyway.
The action looks simple, but looks can be deceiving. Both of these terms are hide-behind-the-couch complex. R is the Ricci scalar. The Ricci scalar is a contraction of the second rank Ricci tensor. The Ricci tensor is itself a contraction of the fourth rank Riemann curvature tensor. The Riemann curvature tensor is the sum of two differences: derivatives of Christoffel symbols and the product of two Christoffel symbols, where a Christoffel symbol is a contraction of three different derivatives of a metric tensor.
Is there a big picture view of this technical monster? Notice that because there is a derivative of a Christoffel which has derivatives of a metric, there are second-order derivatives of the metric tensor. The entire collection transforms as a tensor. Math masters showed long ago that the Riemann curvature tensor is the simplest tensor with second order derivatives of a metric.
That claim though has struck me as both true and odd. The only reason one introduces the need for a connection is in the context of a covariant derivative. A second order covariant derivative will necessarily contain a second-order derivative of a function as well as a second-order derivative of a metric.
To get a sense of how fantastically complex the Riemann curvature tensor is, count the number of metric symbols that are involved (there is only one metric under the math microscope, but looked at a great many ways). In four dimensions, a rank four tensor has 44=256 terms. Each of these has 6 Christoffel symbols (6x256=1,536). Each Christoffel has 3 derivatives of a metric and one contraction. The grand total of metric symbols in the Riemann curvature tensor is 6,144.
The Jedi Masters of differential geometry will say that by harnessing the power of the symmetries inherent in the Riemann curvature tensor, one can greatly reduce the complexity. I do not doubt the truth of their words. I have read those chapters in general relativity books, but could not honestly follow all the details. It strikes me as odd that the reduction is necessary. One would naively hope that the one fundamental long-range force with but one charge would be a direct construction.
The Field Equations
I feel that I could teach anyone who knew high school algebra and had a semester of calculus how to derive the Maxwell equations. It is an interesting game of mathematical sudoku. For me, the same does not apply for deriving the Einstein field equations from the Hilbert action.
I did devote a blog to the subject. I have now reviewed its content which was essentially taking a wikipedia entry on the topic and rewriting it myself to get me to work through the details.
I have a single sheet of paper with the derivation of the Maxwell source equations using quaternions. For this blog, I created a similar sort of 1 page cheat sheet for deriving the Einstein field equations from the Hilbert action. Look at them side-by-side (print out from the links if you want to see the detail).
Other than the fact that the two start from actions, there appears to be no similarities between the two long-acting fundamental forces of Nature. For gravity, one uses the product rule and a few technical facts about Riemann geometry. For EM, it is all about the squares of derivatives of potentials. I don't like the dichotomy. In my opinion, the difference in the actions may justify the stalemate that has prevented unifying gravity with EM and thereby the rest of quantum field theory.
In EM, the interaction term is simple: the charge sits next to the potential. To derive the field equations, vary the potential and all that remains is the current density. Easy-peasy lemon squeezy.
For general relativity, the interaction term is written simply as Lm. When doing an integral in flat spacetime, the variable of integration, , works fine. In curved space-time, volumes are altered, so the variable of integration needs to be
. The little alteration plays a key role. It really should be written right next to the other big players:

The metric stuff is sitting next to the mass stuff. This strikes me as quite unusual. Typically one only needs to drop the Lagrangian in the Euler-Lagrange equation. This time it is the Lagrangian times the change in volume factor from the variable of integration. Gravity is about space-time geometry, and the geometry lives in the square root of the determinant of the metric.
Note: I am still struggling with the matter Lagrangian. I feel completely comfortable in EM with the EM Lagrangian and the path to the field equations because I can write out all the terms. I have not reached the same level of understanding here. In fact, in my hope to find a way to write the matter Lagrangian in components, I mangled things. I am putting text in a box as a sign that it should be skipped.
I have confessed in other blogs about fearing the complexity of the stress-energy tensor. The stress-energy tensor gives me stress. This is reasonable particularly in the context of general relativity. The stress-energy tensor I am confident about is the one for an uncharged, non-rotating, spherically symmetric source: only the T00 term is not zero, and it is the mass density of the source. The simple source leads to the comparatively simple Schwarzschild solution.
If all one does to the source is to rotate it, there is an exact solution called the Kerr metric. It took more than forty years to find this solution. The details look scary to me. Perhaps I frighten easily. Every mass in the Universe spins, but I doubt the Kerr metric is used in practice often due to its complexity.
A stress-energy tensor that gets used in cosmology is the pressure-less dust:
So long as nothing interacts and there is no pressure, a few solutions to the Einstein field equations have been found for this stress-energy tensor. But don't let the dust rotate or the solutions no longer work. The number of solutions to the Einstein field equations is limited.
The Equations of Motion
The equations of motion are generated by varying the action with respect to position and its derivative, velocity. The Ricci scalar R is all about the metric and how it varies, not about position or velocity. What I have not seen is an explicit reference to the stress-energy tensor. Apparently authors think readers of such technical literature should just "know" what is going on. I suppose that is fair, I am stretching on my tip-toes to see what is on the grown-ups table. What I saw were two different actions written for the equations of motion:
or
For months on end, I struggled with how there could be two expressions. The relationship to the Hilbert action was not apparent either. Fortunately some fog has cleared. The first expression is about kinematics, hence the subscript k. Kinematics is all about the motion, not explicitly about energy or momentum conservation. Vary the kinematic action, and the result is an extremum for the path length. Because the action is about path length and not explicitly about energy, there is not a direct road to the Hilbert action.
The second action is the stress-energy of an isolated particle that needs the dynamic metric to carry out the contraction. Thus it is the Hilbert action applied to a very specific situation. Neither happen to feature the Ricci scalar because it will not make a material contribution to the equations of motion (unlike the case for the field equations). I was slow to pick up on the distinction between the action for the field equations and the equations of motion. Of course it is the same action. What changes is the system and its description. For the field equations, one assumes the source is static, uncharged, and spherically symmetric. For the equations of motion, the test particle is dynamic, but is a minor player.
The action looks quite different depending on the situation. Here is the uncharged, non-rotating, spherically symmetric action:
I added the "k" as a stand in for constants needed to make the units the same (inverse distance squared for R, mass/volume for rho). All the energy that alters space-time geometry is contained in one value, rho.
Here is the same action under a different physical condition. This time it is a test particle moving through a vacuum. The same action under this different circumstance for a small test particle is:
I wondered for a long time what to say about these two actions. This was a source of some of my confusion in an earlier proposal. The actions look so different. Granted I maximized the difference by not using the Einstein summation convention and writing it all out longhand, something rarely done.
Why the stark contrast in form? Physically one is describing totally different situations. The first one is all the energy pitching in to bend space-time. The second one is approximately no energy responding to the bending of space-time. I could have added up so many particles in the moving test case that I could have integrated over a volume of space-time instead of using a parameter. I feel though that does not reflect how the equation is thought about: how does a free particle respond to a gravitational field? One can see it is all a bunch of energy terms that get tweaked by a dynamic metric solution, the particular values for the metric tensor at a particular place in space-time.
The Future of General Relativity
General relativity is a successful scientific theory. Using a few starting assumptions, it is able to pass an impressive array of observational tests. Light, which has no rest mass but does have equal parts energy and momentum, is bent by gravity as predicted by GR not Newtonian theory, at least to the level measured today. Before the advent of GR, the precession of the perihelion of Mercury was a problem. Before the advent of Star Trek, the planet Vulcan was proposed to hide on the other side of the Sun to add the needed wobble. Einstein was giddy for three days when he realized GR eliminated the need for that dark planet. The prediction of gravity waves is inferred from the energy loss seen in binary pulsars. The recent success of the BICEP2 to spot the imprint of gravity waves is impressive.
Yet general relativity has big failures. The velocity of clusters of galaxies is too slow to be accounted for. The rotation profile of thin disk galaxies is in conflict with observation. The big bang is unstable mathematically. There is no reason why the cosmological background radiation has the same velocity everywhere to one part in ten thousand. Currently, stars are not slowing down on a cosmological scale, but are speeding up.
I don't recall reading anyone else saying clearly that general relativity is not consistent with our observations of the above systems. What I have read many times is the promotion of three different hypotheses which will preserve the vaulted status of general relativity by introducing HUGE amount of "secret sauce" matter that fixes the problems of gravity yet so far has no sensible home within the standard model and cosmic evolution.
I remain convinced that general relativity, a successful physics theory, needs to be replaced. The only way to stump the best physicists of every generation since 1930 to unify general relativity with the rest of physics is that it cannot be done. The side-by-side derivation of the GR and EM field equations why the gap is too great. And GR is not consistent with all observations of the cosmos. While I know the names of the three hypotheses to fix the described problems, I find the claim "we only know 4% of all matter" abhorrent. In the past, astronomers made a valiant effort to find the planet Vulcan hiding behind the Sun, claiming serveral times that it had finally been spotted. They kept hunting while the main proponent was alive. It was general relativity that eliminated all need for the new planet. The good astronomers of today will continue the hunt for dark matter, dark energy, and the inflaton until a new proposal for gravity arrives.


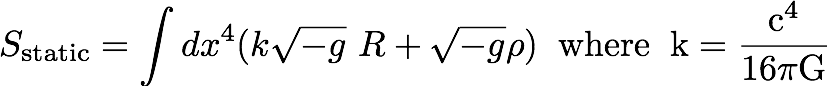


Comments