Today I wish to offer you, dear reader, the chance to contribute to scientific research in particle physics. And I claim you can do that by only leveraging basic high-school knowledge in mathematics and geometry. Let me explain what the problem is, first of all, and then I'll put you in the conditions of contributing!

Muons are subnuclear particles of high interest in collider physics. I could write about muons for ages, but it would not be of relevance for our problem of today, so let's just say they interact feebly with matter, so they traverse thick layers only depositing in them small amounts of energy (mainly in the form of electromagnetic radiation).

Let us take a 2-meters-thick block of matter, segmented into 50 4-cm-thick layers along the z coordinate, and each further divided into a regular 2D xy grid of small 3mm by 3mm cells. Each cell can individually record the energy deposited in it by a crossing muon. Further, the block is immersed in a 2-Tesla dipole field along the vertical y axis, so that a positively-charged muon impinging orthogonally on the front face of the block will then follow a circular path bent toward the positive x direction, with a curvature radius depending on its energy; the dependence is E = 0.3 B R, with B=2T the field, R the radius in meters, and E the energy in GeV.

Our task is to construct an estimator of the curvature R (and thus of the muon energy E) using the measured energy of each detector cell, E_cell[x][y][z]. The problem is that most of the cells of our detector, often not even those along the path of the muon, do not record any deposited energy. Further, photons radiated by the muon may leave a signal in cells far away from the track path. On the average, however, there is an accumulation of energy deposits along the path. You can see an event display of energy deposits below.




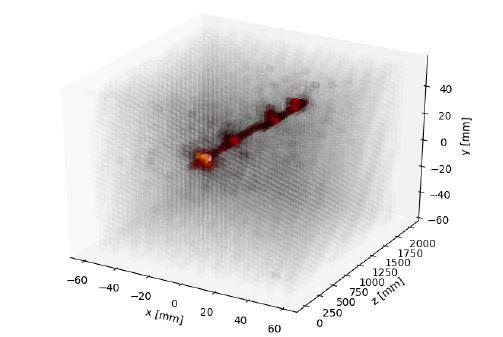
A first -easy- bid to estimate the muon energy is to divide the detector in two 1-meter-thick sections, and determine the center of gravity of the deposited energy in each, thus:







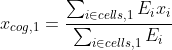
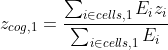
and similarly for the second section. What do we do with these centers of gravity? We can estimate the radius by solving the geometrical construction below:





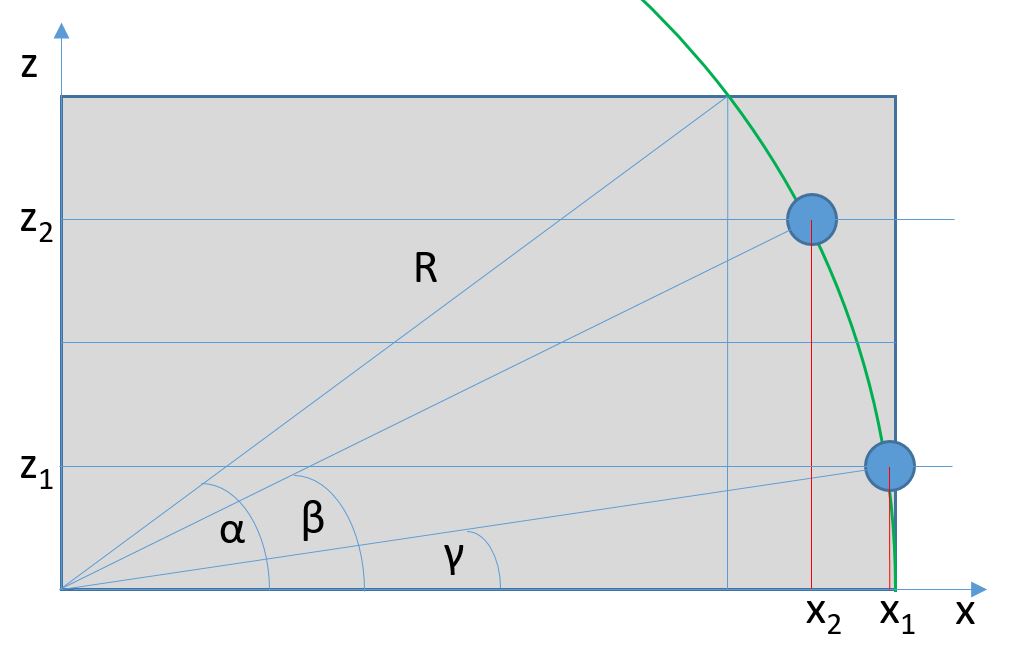
Above, you can see the muon track (in green) and two barycenters (blue circles) in our device (the detector continues to the right, but here only the part to the left of the muon track is shown). We may estimate from the equations above the value of x1, x2, z1, and z2 identifying the barycenters, so we can compute a relation between dx = x1-x2, dz=z2-z1, and the angles, as follows:







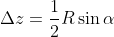
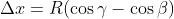
From the above equations, and assuming (an approximation!) that z1, z2 have an expectation value, for a curved track, at positions






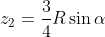
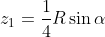
we may work out the value of R by first expressing the angles beta and gamma as a function of alpha, and then expressing cosines as sqrt(1-sin^2). What we get, in the end, is:




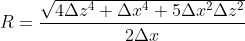
Note that above we are using (approximated) expectation values of the deltax, deltaz distances. In real life, the centers of gravity will be scattered around, because of the stochastic nature of the process of electromagnetic radiation and detection. On average, though, the procedure works, and one may work out an estimate of the muon energy from R by substituting the centers of gravity in the equation above. The result, for muons in the energy range [0,1000] GeV, and B=2 Tesla, is the following:




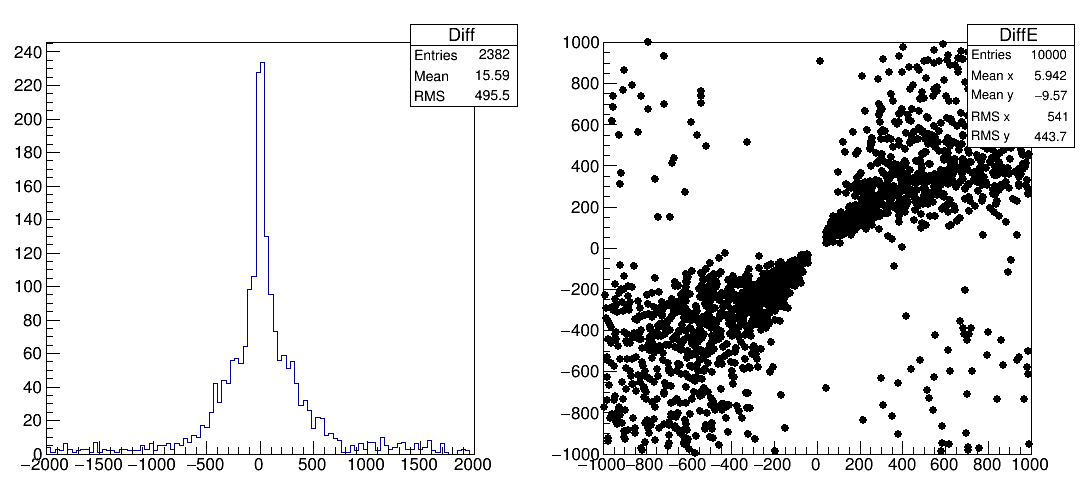
On the left, the difference between true and estimated energy is plotted in a histogram; on the right, the true energy is on the x axis and the measured energy is on the y axis. You can see that the measurement has a resolution below 100% on the estimated quantity. Of course, measuring low-energy muons, which bend more, is easier - for very energetic muons this technique breaks down.

Ok, so - that is what one gets with the simple determination of a circle from two points. The problem is how to improve on that calculation. One could certainly put in a likelihood fit all the individual energy deposits read by the detector, but the fit has a hard time converging, with such a noisy input. Better is to try to construct estimators with geometric means such as the one above. 

If you have care for the details, you will have noticed that above an assumption is made on the expected positions z1, z2 (laying at 3/4 R sin alpha and 1/4 R sin alpha) which is incorrect, as the energy deposits along the detector must depend on the length of the arcs - and the length of the arc per unit depth increases as one considers increasing depths in the detector. In addition, one might improve on the above construction by cooking up analytical R estimates from centers of gravity in three, or four, or even five different sections along z. Not 50 as the granularity of the detector, because as I mentioned, the energy deposits along the muon path are rather discontinuous; but maybe 4 sections would still make sense.

Another detail is that in constructing the x and z centers of gravity above I have used _all_ the cells detecting some energy. Since the track lays in the xz plane, perhaps it would make sense to weight less the energy deposits at an y value much different than that of the track (but the y of the track also needs to be estimated from the deposits!).

If you post in the comments section your own bid for an estimator of R given the vectors of energy and position readouts E_i, x_i, y_i, z_i, I will run it with my simulation and produce a graph such as the one above. The winning solution will be the one with the smallest RMS of E_true - E_meas.

I can offer a Science 2.0 mug as a prize to the winner!