On the matter you of course know well my opinion: as CMS has been measuring two very consistent mass values for the two Higgs boson decay modes, with accuracy superior to that of ATLAS and with combined mass right in the middle of the two ATLAS determinations, the 2.5 sigma effect is certainly just a fluke or some unknown systematical bias affecting the ATLAS results.
While we wait for more data to decide the issue of whether we are in presence of two distinct resonances or not - we will be collecting more Higgs bosons in 2015 than we have in our hands so far - it is nice to see a reanalysis of the ATLAS Higgs samples, which is the experiment's final word on the mass of the Higgs boson based on the 7- and 8-TeV proton-proton collisions collected until 2012. This has appeared as a preprint two days ago. I should be precise and say that it is not just a reanalysis: ATLAS has added some 33% more statistics in this measurement, coming from the latter part of the 2012 run.
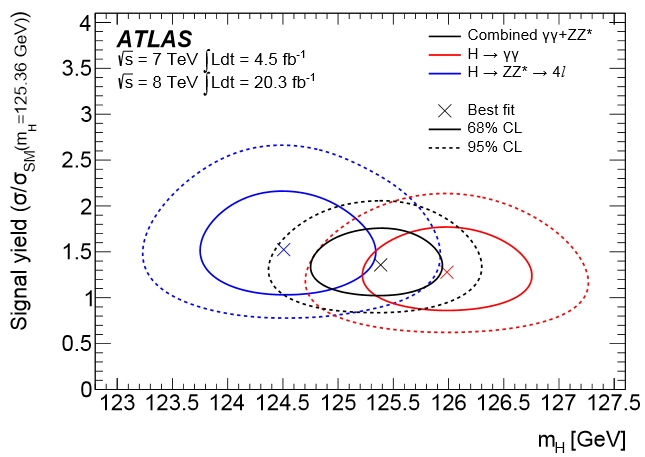
The bottomline of the complex and very detailed measurements made by ATLAS is summarized graphically in the figure below, which shows 1- and 2-sigma contours on the mass versus signal rate plane. You clearly see that the ATLAS data insist on finding two distinct minima for the two datasets, although they have gotten a bit closer than they used to be.
The two mass measurements are quoted as follows in the paper:
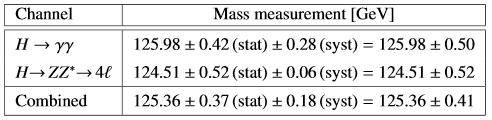
You can see that the discrepancy is almost exactly at the 2-sigma level today. One interesting thing to notice is that while in the past ATLAS result the H->gamma gamma rate measurement was higher than the H->ZZ one, now it is the opposite. The reanalysis anyway finds results compatible with the old ones, if a bit more precise due to increased statistics.
So is it one particle or two particles ? Well, of course it is just one particle ! But the funny twin peaks of ATLAS will live on for another year or two, I suppose. If the 2015 data will insist in showing a difference between the determinations using the two final states, the conclusions we will be forced to draw is that there is a well-hidden, nasty systematical effect that spoils the energy scale of the ATLAS detector (either the photons or the leptons) at the level of 1%... But we are not there yet!





Comments