Modern physics has disproved direct realism: There is no locally realistic description of our world possible. Although I have already explained this differently at several places, for example by refusing 'real stuff' as being a good explanation for what is ‘at the bottom’, it is worth to prove it once rigorously. Let me present the simplest established proof in the simplest possible version that I can come up with. Everybody claiming interest in the interplay between science and philosophy should have gone through this proof at least once and I did my utmost to make it as easy as possible: Only three angles are considered and probabilities almost completely avoided by instead talking about natural numbers like 50. What local realism actually refers to should become obvious along the way.
Imagine a source of pairs of photons (quanta of light). One photon is send to Alice who resides to the left. The second photon is send to Bob, who is far away to the right. Alice has a calcite crystal that has one input channel for her photon and two output channels: One output is labeled “Horizontal” or “H” and the other output channel is labeled “Vertical” or “V”. Photons exiting these channels are horizontally or vertically polarized relative to the crystal’s internal z-axis. Every photon either comes out of the H-channel, in which case her measurement is labeled “1”, or it comes out of the V-channel, in which case her measurement is “0”.
Bob has the same kind of crystal-thingy and so we will write every combined measurement as (A,B) with A being the value that Alice measured and B the value that Bob has gotten. So there are exactly four possibilities for every photon pair: (A,B) = (0,0), or (0,1), or (1,0), or (1,1).
The important point to understand is: Every photon pair is prepared in such a way that if the crystal axes of Alice’s crystal is parallel to that of Bob’s, only the measurements (0,1) and (1,0) ever result!
That such is possible has to do with the conservation of angular momentum of the photon pair and so on and is basic physics – no big mystery involved here. I am not going to somehow “prove” such basics, because you could in principle go into the laboratory and check it yourself. We accept these measurements and photon pair preparations as daily laboratory routine and go on to prove non-locality from it (not that the earth is round or that light velocity is constant or anything else, but only non-locality).
Now it may come in handy (but it is not necessary) if you know a little optics (skip this paragraph if you like): Linearly polarized light that has its polarization axis at an angle of δ (delta) to the vertical (z-axis) and that hits a linear polarizer whose polarization axis is along the vertical, will be attenuated. Why? The projection of the electrical field vector E of the light onto the vertical is proportional to cos(δ). The orthogonal sin(δ) component is absorbed and the left over energy is proportional to the square of E. Thus, the energy left after passing the polarizer is proportional to cos2(δ).
However, the more fundamental description rests on the fact that the discussed crystals do something very similar: If a linearly polarized photon is going into the entrance channel and the relative angle between a certain crystal axis and the photon’s polarization is delta again, the probability to exit as a horizontally polarized photon through the H-channel is cos2(δ), and the probability of going through the V-channel instead is sin2(δ). The combined probability cos2(δ) + sin2(δ) = 100%, as it of course it must be in order to account for all cases.
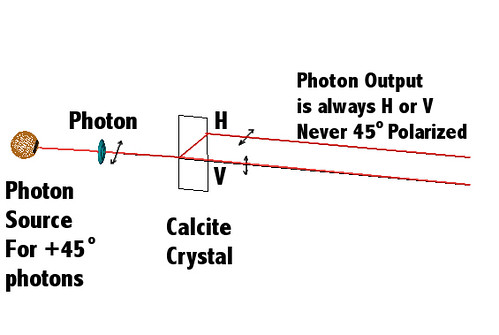At 45 degrees input polarization, the probability to have the photon come out horizontally polarized is 50%.
With other input polarizations, the probability can be adjusted from zero to unity.
Let us recall the paragraph before the previous two: If Alice’s crystal has its internal z-axis at φ0 = 0º and Bob’s crystal is aligned with φ0 = 0º, too, then only the measurements (0,1) and (1,0) ever result! If the crystals are at an angle δ = (φBob – φAlice) relative to each other (twisted along the x-axis so to say), then the outcomes depend on the relative angle δ in precisely the way you would expect from usual optics: the results (0,0) and (1,1) become possible and their occurrence counts increase proportional to sin2(δ).
Say we do this experiment 800 times. Every experiment starts with the preparation of a pair of photons. When the photon going to the left is maybe about half way on its path to Alice’s crystal, Alice randomly rotates her crystal either so that the crystal's internal z-axis is at φ0 = 0º or at φ1 = 3π/8 = 67.5º. Similarly, after the preparation of the photon pair but before the photon going to the right is about to arrive at Bob’s crystal, Bob randomly puts his crystal either at φ1 or at φ2 = π/8 = 22.5º.
Didactic point: No other angles will be considered. The relative δ angles’ magnitudes are thus zero, one, two, and three times φ2, but realists claim that the photons only know about locally present absolute angles, and disproving them is the main issue! This is why I label henceforth with both φ instead of oversimplifying with a single δ label.
Alice and Bob pick the angles randomly. Each has two different angles to choose from, so there are four different combined choices, and they are all equally likely. Hence, out of the NTotal = 800 experiments, about 200 times, a quarter of all cases, Alice’s and Bob’s angles are in the configuration φAlice = φ0 while φBob = φ1. I write thus N0,1 ~ 200. The other three numbers are obviously N0,2 ~ 200, N1,1 ~ 200, and N1,2 ~ 200. Actually, since it is all random, numbers like 195 or 203 may often result instead of exactly 200. Thus, we do not use an equal sign “=” here, but a “~”, which means that the numbers will be pretty close to 200.
What about the outcomes of the measurements? Well, lets enumerate first the N1,1 cases, because for all of them the relative angle δ = (φ1 – φ1) is zero, and that means only (0,1) and (1,0) can result. We write, in surely obvious notation, the expected numbers as
N1,1(0,0) = 0
N1,1(0,1) ~ 100
N1,1(1,0) ~ 100
N1,1(1,1) = 0
The total is indeed 200. These numbers will not be important later on and serve merely as an introduction of the general method and its consistency. It helps to compare with the following four lines and appreciate the fact that the above four lines fundamentally result from them:
N1,1(0,0) = N1,1 * Sin2(0)/2 ~ 200 * 0
N1,1(0,1) = N1,1 * Cos2(0)/2 ~ 200 * 1/2
N1,1(1,0) = N1,1 * Cos2(0)/2 ~ 200 * 1/2
N1,1(1,1) = N1,1 * Sin2(0)/2 ~ 200 * 0
Lets enumerate the N0,1 cases where the relative angle δ is φ1. The expected numbers are
N0,1(0,0) ~ 200 * Sin2(3π/8)/2 = 85
N0,1(0,1) ~ 200 * Cos2(3π/8)/2 = 15
N0,1(1,0) ~ 200 * Cos2(3π/8)/2 = 15
N0,1(1,1) ~ 200 * Sin2(3π/8)/2 = 85
The total is again 200. Only N0,1(0,1) ~ 15 will be important.
The N0,2 cases are very similar. The relative angle δ is φ2, and so the expected numbers are
N0,2(0,0) ~ 200 * Sin2(π/8)/2 = 15
N0,2(0,1) ~ 200 * Cos2(π/8)/2 = 85
N0,2(1,0) ~ 200 * Cos2(π/8)/2 = 85
N0,2(1,1) ~ 200 * Sin2(π/8)/2 = 15
The total is again 200 and only N0,2(0,1) ~ 85 will be important.
Lastly, we enumerate the N1,2 cases. δ is now – π/4 = – 45º. The expected numbers are
N1,2(0,0) ~ 200 * Sin2(–π/4)/2 = 50
N1,2(0,1) ~ 200 * Cos2(–π/4)/2 = 50
N1,2(1,0) ~ 200 * Cos2(–π/4)/2 = 50
N1,2(1,1) ~ 200 * Sin2(–π/4)/2 = 50
Remember that every number counts particular outcomes in a total of 800 trials. The important end result is that N0,2(0,1) ~ 85 alone is by more than 20 occurrences larger than N0,1(0,1) and N1,2(1,1) combined, which only sum to 15 + 50 = 65.
What we have introduced here are the facts as they are experimentally observed. The next time, we will tentatively assume that the world is real and that everything depends only on what is locally present in the vicinity; that Bob’s random decision does not influence Alice’s random choice for example. We will try to reproduce the above result “classically”, so the next time will be much easier than today (the hard part is over!). We will discuss Bell’s famous inequality [1], which states something totally obvious, namely that (N5 + N7) alone is smaller or at most equal to (N6 + N7) + (N1 + N5) combined.
However, (N5 + N7) will equal our large N0,2(0,1) while (N6 + N7) will equal the tiny N0,1(0,1) and (N1 + N5) will equal the small N1,2(1,1). In other words: Local realism cannot possibly describe the world as it reveals itself to us in the laboratory. Put differently: Local realism demands that 85 is smaller than 15 + 50, which implies that local realism is reserved for the crazy among us and that the world is non-local and in a sense not real; it rather exists in our minds!
(That modified realism may be a better conclusion than non-locality is discussed in Part 3.)
-----------------------------
[1] J. S. Bell, "On the Einstein Podolsky Rosen paradox," Physics, 1(3) 1964 pp. 195-200. Reprinted in J. S. Bell, Speakable and Unspeakable in Quantum Mechanics, 2nd ed., Cambridge: Cambridge University Press, 2004; S. M. Blinder, Introduction to Quantum Mechanics, Amsterdam: Elsevier, 2004 pp. 272-277.
More appetite for reading about that reality does in a sense not exist? Here you go:
Quantum Perspective of the Nonexistence of Light
The World is not woven from Real Stuff
Why There is Something Instead of Nothing
If Schrödinger's Cats All Die, Do the Alive ones go to Hell?
