Duality is one of the most important insights in physics and philosophy of physics. What does duality mean? It means that there are dual descriptions of one and the same observed physics. Duality implies that you cannot possibly decide whether the one description T or the other, to T dual description T’ is right or wrong, because both descriptions lead to the exact same observations for the observers who live in a universe that can be described by the theories T and T’. Both are equally right or wrong, as they are dual descriptions. This is not about interpretation or the often abused Ocham’s razor, since dual descriptions are transformable into each other. They are the same although they look incompatible.
Why is duality relevant? In philosophy of physics, they are still publishing about the “hole argument” in general relativity, unaware of what is going on at the cutting edge. In blogs and pop-science, people ask about how many dimensions the universe really has: two, four, 10? Grasping duality elevates you above these discussions.
Duality had its heyday in string theory, where there are several types of dualities. Wise people may have known the gist of duality thousands of years ago, but now we have mathematical models that show the validity and consistency of such. One such duality is for example the Maldacena (or “AdS-CFT”) duality, proposed by Juan Maldacena.
I met Juan before he became really famous, and I asked him a really stupid question about this duality; I hope he forgot all about it. Maldacena’s duality is about a universe that is described by general relativity inside but by a non-relativistic theory on the boundary around the universe on “the outside”:
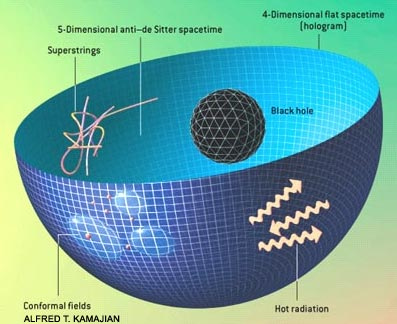
You either describe the stuff inside with general relativity, or you can equally well describe just corresponding “degrees of freedom” on the surface around the universe. The observer does not know whether she lives inside the universe or whether she is made up from stuff on a surface “around the universe”. The universe inside may not "exist" in any sense more than just as implied by what is happening on the boundary surface.
I wrote the previous sentence to make you for a moment think about that possibility, as if it makes sense, which it does not, because it comes better: there is no difference between the descriptions. Being on the surface or being inside, these are the exact same situation! I will describe this in a post on the black-hole instantiation of this kind of “holographic duality”.
Note well: a sphere’s surface is only two dimensional while the interior has three dimensions. The boundary around something has one dimension less than whatever is inside!
So let us put it yet again in another, more pointed way: There is a surface of N dimensions without general relativity, the stuff of which obeys some rules that allow for evolution and all that, only to end up with conscious systems that argue in all earnest that the world fundamentally must have N+1 dimensions and that anybody who does not pledge full allegiance to general relativity as the fundamental last answer is a total quack.
This is basically the state today, and the sad part is: we already know this for quite a number of years. As always, progress goes on funeral by funeral, established philosophers are mostly windbags, and pop-science sells via time-travel and worm-holes, but fails to communicate insight.
The holographic description is two dimensional, as it has only two space dimensions. That does not mean that the world is actually two dimensional. The world does not have two, four or 10 dimensions. The world does not have any specific dimensionality at all. Our descriptions have.
This holds also for the description that has evolved as being the model of our world used by our brains. It looks three dimensional because this is the most useful way to model it in order to eat, have children, and so on. That does not mean that the world is three dimensional.
--------------------------------------------





Comments