Obviously, the young fisherman interprets the data in the context of a flawed model. A model that ignores the importance of evaporation. When evaporation is taken into account, the coincidence disappears altogether. Future generations will also be able to live on land, and past generations did have the opportunity to fish. The fisherman's generation is not special in any way.
Copernican enlightenment
At a dark cloudless night, when we look up at a sea of stars, we tend to ponder as well. But we know better than the young fisherman. Right? We are enlightened. Copernicus taught us something profound: if you think your situation is special, you should probably think deeper.
So we are deeply aware of the fact that we are situation is not special. Our planet is an average planet orbiting a mediocre star whirling with many billions similar stars in a giant vortex. A vortex of stars that is most ordinary amongst many billions of similar vortices that make up the cosmic sea we live in. There is absolutely nothing special about our position in the universe.

Where is our sun? Don't be bothered. The Copernican principle tells us you might as well try to spot your particular piece of hay in a haystack! (Image: Jon Lomberg -- Portrait of the Milky Way)
Cosmologists have elevated this idea to a fundamental principle rather unimaginatively named the cosmological principle. Simply put this principle says: on a cosmic scale there is no special place. The distant sky looks the same from each position in the universe. The immediate consequence of this is that if your theory requires observers on earth to occupy a special or privileged position within the universe, your theory is deemed to be wrong.
This cosmological principle forces us to adopt a non-anthropocentric view that immensely simplifies our description of the universe. It is at the very foundation of modern cosmology and integral part of the standard model of cosmology that describes the big bang and the cosmic expansion.
But there is a snag.
Since Einstein we know that we can not consider space as a entity separate from time. Space and time are inseparable. Or as Hermann Minkowski put it most eloquently a century ago:
"Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality."How does the cosmological principle gel with the Minkowskian principle of unified spacetime?
It doesn't.
The cosmological principle separates space from time. It dictates our position in space to be mediocre, whilst allowing our position in time to be very special. Cosmologists tell us we are a very special generation privileged to live in a highly unique window of time.
Sound familiar?
The standard model
Deep space observations have profoundly changed our view on the universe. This has resulted in what is referred to as the standard model of cosmology, the Lambda-CDM model. According to this model current times are absolutely unique. It tells us that the recently observed acceleration of the cosmic expansion just kicked in, and that it is only around the current age of the universe that this acceleration can be observed. At earlier times the acceleration would have been too small to be observable, and at later times distant galaxies will have accelerated out of view and thereby rendering the cosmic acceleration again unobservable. The cosmic acceleration happens to be observable around the time cosmologists populate planet earth.
What is the ingredient in the Lambda-CDM model that is responsible for this coincidental acceleration?
To answer that question, we need to wind back almost a century, to the time when Einstein was trying to get his newly derived theory of gravitation to describe the cosmos. In a misguided attempt to get a description for a static universe, Einstein introduced a cosmic tension in his theory in the hope that this tension could balance the gravitational attraction so as to render a static universe. When a decade later Edwin Hubble observed the universe not to be static but rather to expand, Einstein realized he could have predicted such a non-static universe, would he not have introduced the cosmic tension fudge factor into his theory of gravity. Einstein henceforth referred to the introduction of this cosmic tension as 'his biggest blunder'.

Hubble watching Einstein being confronted with his 'biggest blunder'
At the very end of the twentieth century, decades after Einstein's death, cosmologists found themselves with their backs against the wall. Faced with the unexpected observation of the cosmic acceleration they saw no other way out than to re-introduce Einstein's biggest blunder. Driven by further observational evidence, a slightly more generic form of cosmic tension, referred to these as 'dark energy', quickly gained prominence in mainstream cosmology. By tuning the dark energy tension such that at cosmic scales it overpowers gravity, a description of the cosmic acceleration results. The resulting model is referred to as the Lambda-CDM* model, a remarkably successful description of the universe. But also a description that leads to a weird coincidence.
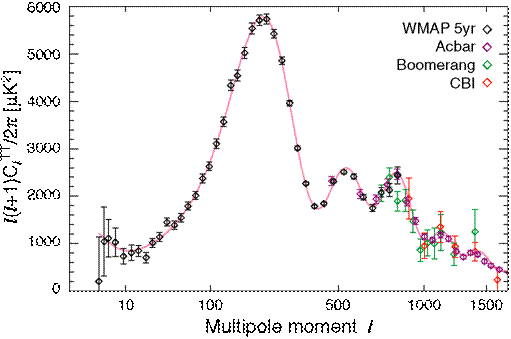
Amongst other feats, the Lambda-CDM model (purple curve) is highly successful in describing the 'echo of the big bang': the cosmic microwave background (the symbols denote measurements on the statistics of its anisotropy).
Quantifying the Coincidence
So we have a highly successful cosmological model hampered by a bizarre coincidence. But how bizarre is this coincidence really?
Let us put some numbers in. What is the current age of the universe? Expressed in natural units, about 1061 ticks have passed since the big bang. It is around this very time that we can observe the accelerated expansion of the universe. But only marginally so. It took us four centuries of telescope technology improvement before we managed to observe the cosmic acceleration. Observing cosmic acceleration is challenging, as one needs to look very, very deep into space to see any effect. This is because dark energy represents a cumulative effect. In a rough analogy, one can think of dark energy as a negative mass that increases proportional to volume. For a volume the size of our earth, the dark energy adds up to a negative mass corresponding to removing a single grain of sand from the entire earth.
Tiny as it might be from our earthly perspective, the dark energy effect does grow proportional to volume. It keeps growing with increasing size until we reach the size of the whole observable universe. At that size, the effect has grown from taking away a grain of sand into an effect that overpowers the total mass in the universe. At the scale of the universe, dark energy beats the deceleration due to gravitational attraction, and the result is a cosmic acceleration.
All of this applies to a cosmic age of around 1061 ticks. Earlier on (any time till about 1060 ticks since the big bang) the size of the universe was so much smaller that the total dark energy effect got dwarfed by the forces of gravity. Would we have lived around 1060 ticks after the big bang, we surely would not have observed a cosmic acceleration. Later on (any time around 1062 ticks or later) the acceleration will again be undetectable. This is not due to the relative weakness of the dark energy, but rather due to the distant objects in the universe that currently allow us to observe cosmic acceleration having accelerated out of view.
It is important to realize that we are not just talking practical issues here. Accelerated expansion does not just make late deep space observations impracticable, but rather poses strict fundamental limits. According to the Lambda-CDM model, ultimately all distant galaxies will permanently accelerate out of sight beyond a cosmic horizon that can effectively be considered 'the edge of the observable universe'. It doesn't matter how big a telescope future generations will be able to construct, if all distant galaxies have accelerated out of the observable universe, those future generations will not be able to even get a hint of the cosmic acceleration.
The net effect of all of this is that we are here just at the right time. Neither earlier astronomers nor later astronomers would be able to correctly predict the dynamics and ultimate fate of the universe. It is only us who can accomplish this feat.
Amongst those interested in science, many hold a clear aversion against the concept of dark energy. Not seldomly, this aversion seems fueled solely by the very term 'dark energy' which carries the connotation of 'ill understood' and 'mysterious'. However, would those dark energy critics become familiar with the feats accomplished by Lambda-CDM, the cosmological model firmly build on a dark energy foundation, I am sure many of them would embrace the model.
But one doubt should stays: how come we, scientific heirs of Copernicus, end up with such a strangely anti-Copernican standard model of cosmology? Are we really living at the very right moment in a mediocre location? Or is Lambda-CDM ready for revision? Should we eliminate Lambda, the dark energy component, from the model?
One thing is sure: any model claimed to be capable of replace Lambda-CDM will face some tough challenges in describing a wealth of highly accurate cosmological data.
* Lambda is the symbol for the cosmological tension Einstein introduced into his equation and stands for the dark energy component that drives the cosmic acceleration.





Comments