Like those three legs they walked around on. Not their fragile-appearing spindly-ness,but their actual three-ness.

Please get Tom Cruise first, please get Tom Cruise first, please get ...
There should be more legs. Around six of them, in particular.
“Look,” you might reply, “it’s an alien ship, and who knows what kinds of principles they’ve uncovered.”
Of course, that’s possible. But another way to look at it is that we Earthlings come in a large variety of body and limb plans, and yet we don’t find the three-limb design anywhere. Perhaps that’s a good argument that aliens wouldn’t build a ship with three legs.
What do we Earthlings do for limb design?
We tend to follow a law, one that may cut across all animal phyla, a law I first published in the Journal of Theoretical Biology in 2001 [ http://www.changizi.com/limb.zip ], and elaborated upon in my first book The Brain from 25,000 Feet [ see final section in http://www.changizi.com/ChangiziBrain25000Chapter1.pdf ].
This “limb law” relates an animal’s number of limbs to the length of those limbs (relative to the body’s size).
When an animal’s limbs are very long relative to its body size, I argued that the optimal reaching-out solution (that uses the least amount of “wire,” or limb material) is to have about six limbs. (This applies to animals with limbs that are approximately radially directed around a perimeter. For animals whose limbs directions are uniformly spread over a spherical surface, the expected number of limbs in this case would be about 12.)
As the animal’s limbs shorten relative to body size, the expected number of limbs rises, with tremendous numbers of limbs when the limbs are very short. (By the way, a snake is consistent with infinitely many infinitely-short limbs – i.e., no limbs.)
More generally, the law predicts that an animal’s number of limbs is inversely proportional to relative limb length. And, more specifically, the law predicts a particular proportionality constant, so that “six” is the solution in the case of really long limbs.
Letting L be the limb length and R the radius of the animal’s body, then k = L / (L + R) is the relative limb length, or “limb ratio”.
The number of limbs, N, is expected to vary approximately as
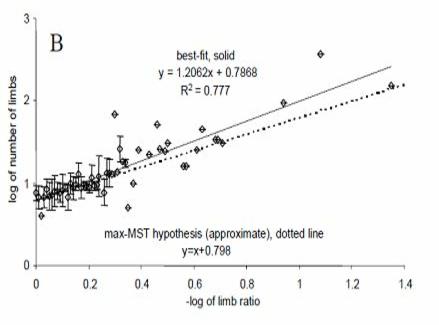
The figure below (from my first book) shows how the number of limbs in fact relates to limb ratio, for 190 species across seven animal phyla (Annelida, Arthropoda, Cnidaria, Echinodermata, Mollusca, Vertebrata, and Tardigrada).
The predicted trend is shown with the solid line, consistent with the N ≈ 6.28k-1 equation we saw just above.
The actual trend is shown with the dotted line, leading to an empirical equation of N ≈6.24k-1.17 … or very close to the prediction.
To get a better impression of the Limb Law that Earthlings appear to follow, check out this little dynamic visual program by Eric Bolz, allowing you to vary limb length and watch how the number of limbs varies: http://www.changizi.com/limb.html The right vertical axis allows you to modulate the limb ratio and watch the number of limbs change. The bottom axis allows you to make longer or shorter creatures. The left vertical axis just allows you to resize the creature on the page.
The alien ships from War of the Worlds should have – given their long limb length and assuming they should be treated as approximately pointing around a perimeter – around six limbs. Not three.
That’s why they look so silly. They’re outside of the sweet spot in design space for limbs.
In my next piece, I’ll discuss how this limb idea tells us why we have 10 fingers, and perhaps, therefore, why we have a base-10 number system.






Comments