To see the Limb Law in action, go to my web site where you can play with an animal’s limb length and watch how the optimal number of limbs changes. Roughly speaking, the animal designs you can create in this program are the ones we find on Earth (…among radially-directed-limbed animals).
The Limb Law applies to more than just animal legs. By “limbs” I refer to any appendages that reach out, and so the hypothesis applies to hands as well, but where a hand’s “limbs” are its digits.
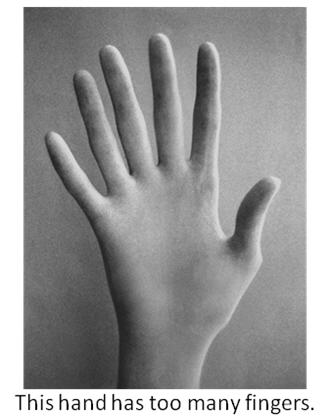
The only thing we must keep in mind in order to apply the Limb Law to hands is that hands are not free-range animals, but are, rather, connected to an animal. Hands have digits pointing away from the arm that connects to the hand, and so have only about half of the digits one would expect if the hand were roaming the world on its own.
In light of this fingers-are-the-hand’s-limbs observation, in this piece I’d like to ask…
In addition to being fundamentally interesting, this question also has deep implications for why we use a base-10 number system (rather than a base-2 or base-8 system, each which would arguably be better).
How can the Limb Law tell us how many fingers we should have, given that it only tells us the relationship between limb length and number of limbs?
Because hands like ours have plausible constraints on how long their fingers should be. Hands must close, i.e., their fingers must be able to reach back over the palm and cover it up. And that simple requirement is enough to enable us to predict roughly how many fingers we should have.
Recall that the Limb Law was that the number of limbs, N≈2π/k, where k was the “limb ratio,” k = L/(L+R), where L is limb length and R the radius of the body.
The demand that finger length be approximately the diameter of the palm means that the finger length should be about twice the palm’s “radius”. So, L≈2R. It follows that k ≈L/[L + (L/2)] = 2/3. And, plugging in k=2/3 into the equation for the number of limbs, N, we have N≈2π/ (2/3) = 3*π ≈ 9.42.
That is, given that fingers must be roughly as long as the diameter of one’s palm, then there should be about 9.42 fingers poking out from the circumference of the palm.
But remember that palms aren’t animals living freely on their own, but are attached to arms, and thus we expect palms to have digits on only about one half of their circumference. So, 9.42 is twice what we should expect for the number of fingers. Divide 9.42 by 2 and we have 4.78 fingers per hand. Or, about five.
Could it be that your run-of-the-mill alien would also have ten fingers, and thus get saddled with base-10?






Comments