The tau was discovered in 1975 by Martin Perl at the SPEAR electron-positron collider. The acceptance of that observation was quite slow: the events found by Perl and his team were complicated because of the peculiar properties of the newfound particle. Perl had found an excess of events featuring an electron and a muon and an energy imbalance, which were hard to explain unless hypothesizing the creation of a pair of short-lived, heavy leptons.
The fact that neutrinos were carrying away energy and momentum prevented a measurement of the mass of the tau. Eventually, however, Perl got his Nobel prize for the discovery, in 1995!
Today the tau lepton is extremely well studied, and although it is much harder to detect taus than electrons or muons in the hadron-hadron collisions of the LHC, the decays can be used to extract meaningful physics results. For instance, one can search for Higgs decays to tau lepton pairs! The graph below shows the signal found so far by CMS.
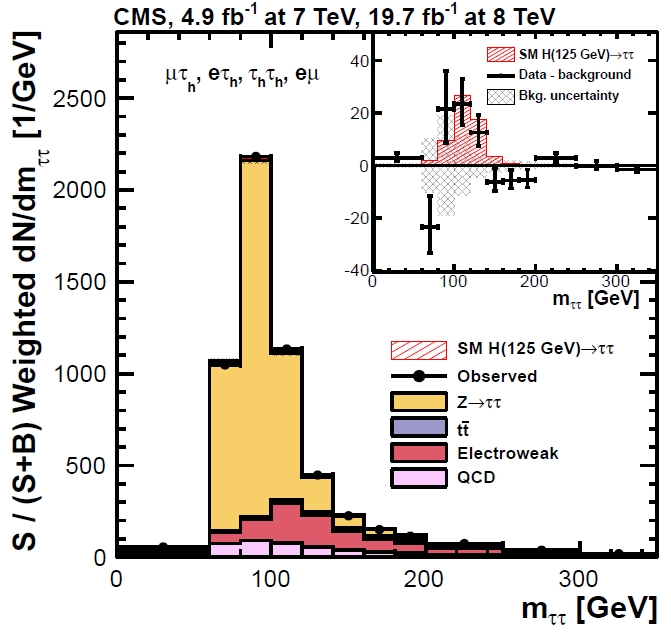
Above: distribution of the reconstructed invariant mass of tau lepton pairs from CMS 2011-2012 data (black points) compared to backgrounds (mostly due to Z->ττ decays, in beige). The upper right inset shows the excess of data over backgrounds, compared to the predicted Higgs signal (red hatched histogram).
Besides the fact that a tau lepton always yields at least one neutrino -a tau neutrino, in fact- in its decay, the other reason why it is complicated to study is that its large mass allows all sorts of decays: not just ones to an electron and two neutrinos or to a muon and two neutrinos, but also ones involving light hadrons. Let me first explain the leptonic decays however.
The tau turns into a neutrino by emitting a virtual W boson. The latter can materialize either a electron - electron neutrino pair, or a muon - muon neutrino pair: in these "fully leptonic" decays the final state has a charged lepton and two neutrinos. They are those which were first spotted by Perl in 1975. In a modern-day detector the signature of a tau pair production (say when the two taus are the product of the decay of a Z boson) can thus be the one seen by Perl, of an electron and a muon of opposite sign, not balancing in transverse momentum. However, there are more frequent decay modes involving hadrons, and those are much harder to spot.
The virtual W boson emitted when the tau turns into its own neutrino, in fact, has enough energy to materialize a few light hadrons: pions, kaons, or even more massive particles. If one looks in the Review of Particle Properties (here), one finds literally dozens of observed decays to hadrons. Most of them have small probability of occurring, but in total they make 66% of the total; the eνν and μνν modes take a share of 17% each.
My general knowledge of tau lepton decays stops roughly there: I know that taus may generate "one prong" and "three prong" topologies whereby there is only one charged particle (of charge, of course, equal to that of the tau) or three charged particles. These charged particles are almost exclusively pions, and they may or may not be accompanied by additional neutral pions. And I know little else.
So I was surprised last night to learn, during a dream, that the tau can also decay to a phi meson! The phi meson weighs 1020 MeV, so the decay of a tau to a phi plus a neutrino and a charged particle is energetically possible; but I had never really thought of that possibility. And I had to dream about it to learn it.
In my dream, I was talking to Luca Perrozzi, formerly a graduate student who worked with my group in Padova at a few early measurements we did with the first data taken by CMS in 2010. One of the early measurements was to detect the very first signal of the phi meson in its decay to kaon pairs - something which is very boring physics in absolute terms, and yet something which at the very start of CMS data taking was interesting to measure, to verify the capabilities of the detector to track charged particles and the possibility of silicon sensors to provide a measurement of particle characteristics through the specific energy loss of charged particles in the sensors.
The phi meson, which decays to kaon pairs, offers the chance to verify that one can discriminate the omnipresent pions from the less frequent kaons using the silicon energy deposition measurement. Indeed, by selecting tracks with "kaon-like" energy losses we extracted a very nice peak with data from the very first few days of running. But that is ancient history now.
Luca nowadays is measuring the W boson mass with CMS data. In his measurement he is using muons and electrons only; in the dream, however, he was also using other signatures. And he was reporting to me that he had two events that he could not really understand: those events appeared to have two kaons making the mass of the phi meson, and one further track of high momentum; and he could not understand their origin; in particular, the phi meson appeared to have a long lifetime - while in truth we know that it decays too fast for its decay length to be detectable.
In my dream we discussed in some detail the events, which Luca appeared to be willing to attribute to W production. And then it dawned on me: these were tau lepton decays to a phi meson, a pion, and a neutrino: the phi thus appeared to have a long lifetime, but that was in fact the long lifetime of the tau (the tau lives only a few tenths of a picosecond, but that is enough for it to travel a few millimeters before decaying). When I explained that to Luca in the dream he appeared convinced that I was right; but a dream is only a dream...
So today I decided to check whether such a decay has ever been studied or seen in a previous experiment: and I was pleased to see that it indeed has been measured. It occurs 35 times every million decays, so it is rare, but not impossibly so. In particular, CMS may well have been collected a few of these events in the 2011-2012 data. Note, however, that a W boson decay to a tau-tau neutrino pair will be hard to trigger on if the tau goes on to decay to a phi and a pion: there is nothing distinctive in the event apart from the missing transverse energy due to the escaping primary neutrino. However, we might have collected some Z->ττ decays with a subsequent decay of one tau to electron or muon, and the other to phi and pion. But how many?
The Z->ττ production rate in CMS is of about one nanobarn, so that means about 20 million such events in the whole data collected so far. Now if we ask for the final state of one fully-leptonic decay (eνν or μνν) and one φπν decay, we should be left with 20M x 2 x 0.34 x 0.000035 = 476 events, okay let's make it 500 to round it off. Now, of those 500 events one may expect that no more than a tenth has been collected by the trigger, as the electron and muon from tau decay do not always have enough energy to pass the trigger threshold, and further oftentimes they will be emitted at small angle with respect to the beam pipe, making their triggering impossible.
That ballpark estimate leaves with about 50 events in the data. It should be possible to select them (in the middle of a really large background!), by requiring the presence of an isolated electron or muon recoiling against three charged particles vertexed together, two of which making the phi mass if assigned the kaon mass hypothesis. But would this be a worthwhile endeavour ? Probably not - the branching ratio of tau leptons into phi and pion is already measured to 15% accuracy, and not much there is left to learn from a more precise determination which would anyway be almost impossible to obtain with CMS.
Still, it is fun to just play with these branching ratios and imagining how many reactions of some particular kind are present in the data that LHC has produced. Or, at least it is sort of fun to me -today you are probably much more interested in what will be said at the Harvard press conference on the B-modes !





Comments