After re-emerging from a rather debilitating new years' eve banquet, I feel I can provide my own answers to the second batch of physics questions I proposed a few days ago to the most active readers of this column.

Be sure about one thing: the answers to the three questions have already been given in some form by a few of the readers in the comments thread; I will nonetheless provide my own explanations, and in so doing I might pick a graph or two to illustrate better the essence of the problems. But first, there was a bonus question included in the package, and nobody found the solution to it. Here is the bonus question again:

"What do you get if you put together three sexy red quarks ?"

The answer is

"I dunno, but I'm getting a haDR-on just thinking of it!"

Okay, leaving such trivialities (for which I have to thank Robyn M.) behind our back, we can now discuss the physics. To make this piece easier to read, I paste below the three questions:

1) The LHC experiments will search for Z bosons in
their early 2010 data. The Z decay to muon pairs, in particular,
provides a means to verify the correct alignment of tracking detectors
and the precise modeling of the magnetic field inside the solenoid,
which bends charged tracks traversing its volume.
If the signal cross section equals 50 nanobarns, and only three decays in a hundred produce muon pairs, calculate the integrated luminosity required to identify 100 candidates, assuming that the efficiency with which a muon is detected is 70%.
Hint: you will need to use the formula , and all the information provided above.

2) In the decay of stopped muons, ,
the produced electron is observed to have an energy spectrum peaking
close to the maximum allowed value. What is this maximum value, and
what causes the preferential decay to energetic electrons ?
Hint: you might find inspiration in the answer to the first question I posted on Dec. 26th.

3) The decay to an electron-neutrino pair of the W
boson occurs one-ninth of the time, because the W may also decay to the
other lepton pairs and to light quarks, and the universality of charged
weak currents guarantees an equal treatment of all fermion pairs. The
question is: if the W boson had a mass of 300 GeV, what would the rate
of electron-neutrino decays ?
Hint: the top quark would play a role...

1 - The first question was the easiest to answer, in my opinion. It is, in fact, a very simple multiplication of the given data, but if you have never done a similar computation you might easily get confused. So let me go over it in some more detail than I would think necessary.

The number of subatomic interactions producing a particular reaction, whose probability of occurring is encoded in its cross section , is indeed obtained by multiplying that cross section by a "flux" factor, described by what we call "integrated luminosity", . Since cross sections are measured in units of area, it is natural that a multiplication of that area by a quantity having units of "number per area" -id est, a flux integrated over time- gives as a result a pure number -the number of collisions producing the wanted process. has indeed units of inverse area, and so we do write , as in the hint above.

Now, we want to know the luminosity needed to see 100 Z decays to muon pairs: to see 100 decays in your detector, however, you have to produce many more Z bosons, because only 3% of them do decay into muon pairs; and further, you get to reconstruct both muons only 70% x 70% = 49% of the time, because of the incomplete acceptance of your detector and the imperfect identification algorithms. So if we want to see 100 decays, we need to produce more: the number is given by , roughly (don't expect that I fetch my pocket calculator for such a calculation!).

So the answer we seek is simply , or 134 inverse nanobarns, give or take a few. It is an integrated luminosity that the LHC will collect in less than a day of running at startup; the same integrated flux is achieved nowadays by the Tevatron in half an hour, but the Tevatron is a perfectly tuned machine -the LHC at full speed should collect it in less than a minute.

I highlighted "give or take a few" above to remind myself of making a point here. Before I go to the next exercise, let me explain one thing about calculations by heart like the one above. Since we want to know the integrated luminosity needed to see 100 detected Z decays to dimuons, we know that we do not need L to be computed with a 1% accuracy, since those 100 Z decays obey Poisson statistics, and therefore even if we knew perfectly the Z cross section, and the dimuon branching fraction, and the detection efficiency, all that precision would be useless: the determined L would be subjected by a random fluctuation of the order of 10% of itself -that is, the intrinsic variability of 100: +- 10.

What I am trying to explain is that the answer to the question, for an experimental physicist, is not "to see 100 Z decays to dimuon pairs we need to acquire an integrated luminosity of L = 134/nb", but rather "to see 100 Z decays to dimuon pairs we need to acquire an integrated luminosity of about 130 inverse nanobarns". The second answer, thanks to the intrinsic inaccuracy which it contains, is -to me- actually more accurate!!! Remember this, because it is an important lesson: the uncertainty is more important than the measurement. In the sentence "about 130" we make it clear that we are not serious about the last digit, and so we provide MORE important and accurate information than "=134"!

Let me stress it again (and I will make it a "say of the week" one day): given a chance to either be given the result of a measurement without its uncertainty, or be told the uncertainty of the measurement without the value of the measurement itself, you should choose the second!

2 - The key to understand the behavior of the weak decay is to realize that the process proceeds through a V-A charged weak current: V stands for "vector", and A stands for "axial-vector". I am not going to start writing down gamma matrices and spinors here: I could explain that to you, but it would take too much of my patience for today.

Instead, let me just try to explain it as follows. We have three final state particles; two (neutrinos) basically massless, the third (the electron) also almost massless. For such low-mass particles the momenta involved make them all ultra-relativistic, so that helicity (the projection of spin along their direction of motion) is a good quantum number: we can use it in our reasoning. Two of the decay particles (the electron and the muon neutrino) want to be left-handed, i.e. have a -1/2 helicity (as dictated by the weak interactions), the third (electron antineutrino) wants to be right-handed, and thus have a helicity of +1/2.

Now let us take a x-axis (do not get scared if I slip into calling it a "quantization axis") as the one along which the original muon spin is aligned: the muon has spin "+1/2" along x. The vector current which produces the weak muon decay "flips" the spin of the muon, such that its sibling -the particle carrying away the "muon-ness", the muon neutrino- has spin opposite to that of the parent. This means that the muon neutrino will travel away in the positive x direction, with spin -1/2 along that direction.

The unit of spin necessary for this spin flip -a "+1" along x-  is carried away by the electron-electron antineutrino system, against which the is recoiling. Since the electron wants to be left-handed and the electron antineutrino wants to be right-handed, then if the two traveled in the same direction they would cancel their spins: but we just said that the system has to carry away a full +1 unit of spin. This is only possible if they are emitted back-to-back, with the electron traveling along the negative x direction (with spin +1/2  along x), and the electron antineutrino traveling along the positive x direction (with spin +1/2 along x again).

We thus have a preference for the decay to yield the two neutrinos traveling together in the direction of the original muon spin, and the electron shooting out in the opposite direction. If that is the case, the momenta of the two neutrino will have to balance the one of the electron. Since the three particles have masses much smaller than the parent mass (105 MeV), their momenta and energies are almost equal. The electron gets an energy of 52.5 MeV, and the two neutrinos share the other 52.5 MeV. The mass of the muon, that is, has been converted in momentum of the decay products (and minimally into the electron mass).

Please bear in mind that the real situation is not so clear-cut as I have described it above, of course: the emitted electron is not perfectly left-handed because its mass is not negligible; and I have considerably simplified the picture by considering the extreme case of a perfect alignment of the three final state particles along an axis, spin flip, etcetera. Despite my inaccurate treatment, I think it appears clearly that there is a preference for the configuration discussed. A sketch of the electron energy distribution from stopped muons is shown on the right: as you see, rather than a fair share of the parent's energy (105/3=35 MeV) the most probable electron energy is higher, close to the maximum allowed value.

3 - This question was rather easy to answer, if you correctly accounted for the fact that quarks need to be counted three times, because there are three different species of each: red, green, and blue (or pick any other trio of colours you fancy). So, a 300 GeV W boson would not just decay into : it would also readily produce  pairs, one per each of the three colours those quarks may take.

Now, the democratic nature of the charged-current weak interaction makes the regular W decay one-ninth of the time into each of the listed pairs; a 300 GeV W would be just as democratic, and each of the now 12 possible final states would get a one-twelfth chance of occurring.

As one reader correctly pointed out (I think it was Lubos), the top quark is quite heavy, and its mass cannot be neglected in the decay. The large mass of the top requires a large "investment" of part of the released 300 GeV coming from the hypothetical W boson's disintegration. This would actually make the mode less probable than the other quark decays! It is a subtlety, but it is useful to point it out. The disadvantage of the top-bottom decay would be due to something we call in jargon "phase space suppression".


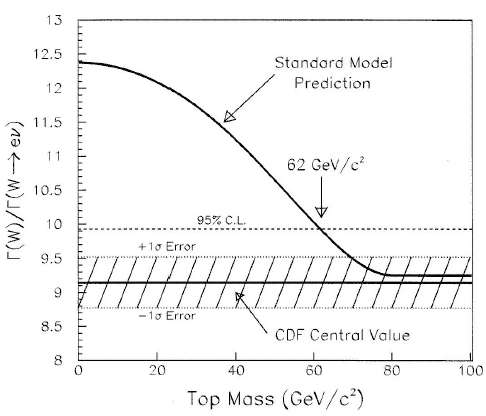
You can see the suppression quite clearly in another calculation, which was done twenty years ago, when the top quark had not been discovered yet. Back then, we did know very well that the W boson had a mass of 80.4 GeV: but the top could still be lighter than the W, so one could compute, as a function of the back-then-unknown top quark mass, the fraction of W decays that would be yielding electrons: this number should be one ninth if the top is heavier than the W, or smaller if the top is lighter. The curve in the graph above shows exactly how the "phase space suppression" acts to make it less and less probable that a W decays into tb pairs, as the top mass gets higher and closer to the kinematic limit (what is shown in the vertical axis in the figure is the inverse of the fraction of W decays to electrons, that is a number close to 9 for a large top mass, or close to 12 for a small top mass).
 
In the figure you see actually a direct exploitation of the very effect of phase space suppression. Since the total number of modes into which the W boson may decay can be inferred by directly measuring its natural width -how thick the peak is, which is a number proportional to the speed of the decay, which in turn depends on the number of possible ways it can disintegrate- the determination of the number of W->electron neutrino decays can be turned into a value on the vertical axis (hatched horizontal band measuring at 9.14+-0.36). That, combined with the theoretical curve shown in black, allowed to give a lower limit to the top mass! The arrow shows the limit, M(top)>62 GeV, at 90 % confidence level (the value corresponding to the 90% upper bound on the hatched relative inverse width, 9.93). The result shown in the CDF figure above was produced twenty years ago, and it is now of only historical value. And didactical, too!