If you know me, you are no doubt positive that I discussed those fluctuations just for the sake of it, to arise interest in the Tevatron searches, and that I do not give two cents to the idea that those fluctuations are due to anything else than Poisson statistics -the intrinsic variability in the number of events that experimental searches collect. Nevertheless, the possibility exists that a new boson will eventually show up like a towering signal in a dilepton mass distribution, one fine day. But why are theorists, and experimentalists alike, considering so seriously the possibility of a new Z' boson ?
While I do not think I need to explain why theorists are anxious to try and extend the standard model of particle physics to accommodate new features, predict new physics, explain away the inconsistencies, and win a Nobel prize, I do wish to remark that the standard model is such a sensitive, precise construct that it is extremely complicated to extend it in a way which does not spoil its perfect agreement with experimental results. It is like trying to hide a bull in a crystal shop: the problem is not so much finding a good hiding place, but rather bringing it inside without breaking anything.
It so happens that a class of so-called "Z' models" can do that; and some of these models have the added interest that they can be tested with data which we expect to come out of the LHC experiments in the next few months. This is in short the main result of a recent paper by E.Salvioni, A.Strumia, G.Villadoro, and F.Zwirner, "Non-Universal Minimal Z' Models: Present Bounds and Early LHC Reach", 0911.1450. I wish to summarize the results of Salvioni et al. in this article; but before I do, I feel the urge to go into some of the details of the theory of electroweak interactions to explain why a single additional massive, neutral Z' boson might be the obvious result of the simplest extension of the standard model.
Of course, you cannot expect that a short description will allow any real understanding of the subtleties of the theory; nor that the standard model can be "explained" in twenty lines of English; nevertheless, I still like to give it a try. Maybe you can just skip the next section if you are running low in attention tokens; the same of course is advised if you have studied the standard model already.
The group structure of the standard model
Elementary particles may be described by complex functions of spacetime (I might slip into calling them "fields": bear with me), composed of a modulus and a phase. The phase should have no impact on the observable characteristics of the particles, because what we experience are intensities, which are real quantities obtained by squaring the particle amplitudes: so in technical jargon, the theory predictions must be invariant under transformations of this phase, to make any sense.
The standard model of particle physics, the wonderful toy which allows us to predict the phenomenology of particle interactions with amazing precision and simplicity, is constructed in a way that retains the invariance of the predicted phenomena upon changes of the phases of the fields. The invariance properties of the observable phenomena under such phase transformations are described mathematically by symmetry groups, which can be combined like logical blocks.
In fact, the symmetry properties of the physics described by the standard model can be summarized by writing down its total group of symmetry, SU(3) x SU(2) x U(1). SU(3) labels a "special unitary group in three dimensions", and it is in our case the group of transformations caused by the quantum chromodynamical interactions between quarks, possible due to the colour charge these possess. SU(3) is really independent on the other two groups, SU(2) and U(1); the latter are instead mixed together by the Higgs mechanism, a choice of the mathematical expression for the state of minimum energy of the system. Until one makes an explicit choice for the state one calls that of minimal energy, the properties of the theory are not apparent; the choice hides the symmetry of the system, but in exchange brings consistency to the whole construct, and crucially evidences mathematically the existence of a Higgs boson field.
The simpler of the two blocks which are mixed together by the Higgs mechanism, U(1), describes the symmetry of the properties of elementary particles making up matter -the quarks and the leptons- with respect to phase rotations proportional to an apparently obscure characteristic they possess, an attribute called "weak hypercharge" Y. The invariance of the phenomena predicted for quarks and leptons undergoing these hypercharge phase transformations is ensured by the existence of a vector boson, which is commonly labeled with the letter B. B is constructed such that its presence in the theory exactly cancels the residual, non-invariant effects caused by the changes of phase which are allowed by the existence of the charge Y.
The other block governing electroweak interactions is the group called SU(2), which describes the transformation properties of fermion doublets. You know what fermion doublets are: fermions come in pairs - up and down quarks, or neutrino-electron pairs; and these pairs are replicated in three different generations. SU(2) doublets are endowed with yet another mysterious charge called "weak isospin": invariance under rotations of this phase in the three-dimensional space spanned by the three orthogonal SU(2) generators demands the existence this time of three weak vector bosons, which are initially labeled W1,W2, and W3. Each of these takes care to cancel the unwanted non-invariant terms in the equations describing the particles of the theory.
Now, the B and W bosons are massless, and this fights common sense, yields a non-calculable theory, and flies in the face of the phenomenology of weak interactions. What is worse, there is no explicit notion of an electric charge in the group structure: where is electromagnetism ?
The magic in the standard model is that by mixing together the W_3 and the B fields, one gets the photon and the Z boson, and as a bonus one obtains masses for the W and Z: the two original blocks, U(1) and SU(2), are mixed by a rotation, whose result are exactly the four vector bosons of the theory: the W+, the W-, the Z0, and the photon. The latter, which is the only boson which remains both massless and electrically neutral, is properly the particle which transmits electromagnetic interactions. As we know, electromagnetism has a infinite range, so it is aptly described by a massless field.
Minimal and less minimal Z' models
Above I have tried to shortly describe the basics of the structure of the standard model. In the literature you usually read that if you want to extend the standard model in the most minimal way (which automatically means adding just one unit of dimensionality to the group of transformation which dictates the phenomenology of elementary particles, a further U(1)' ) this is feasible only at one condition: in order to preserve the many crucial properties of the electroweak theory, the additional group of transformation must bring in a further "charge" which is a linear combination of the original hypercharge Y and the difference between B and L, the baryonic and leptonic numbers of the quarks and leptons.
Perhaps here I should remind you here that quarks have a baryon number of 1/3 each, so that protons and neutrons have baryon number equal to 1 each. Baryon number conservation -the impossibility for a baryon to get rid of their "baryonness"- is what guarantees that ordinary matter is stable, a fact confirmed experimentally with proton decay search experiments. Lepton number L also appears to be conserved, separately for electrons (L_e), muons (L_mu), and tau leptons (L_tau); however, recently the discovery of neutrino mixing has proven that individual lepton numbers are indeed not conserved.
In the recent paper by E.Salvioni, A.Strumia, G.Villadoro and F.Zwirner, the above assumption on the way the charge of the new U(1)' group is constructed is relaxed. The authors note that one can in principle construct a new charge which is a linear combination of Y, B, and separately the three leptonic numbers L_e, L_mu, L_tau, and still manage to obtain a consistent, non a-priori ruled out theory.
Because of the possibility to treat differently the three lepton charges, a model with such a new charge is called "non-universal". Universal is a very specific term in electroweak theory jargon, and it equates to say that leptons always appear on the same footing in electroweak interactions: a very well-established fact experimentally; but there is nothing wrong with speculating that high-energy interactions bringing in the exchange of new heavy Z' bosons might change the picture, and indeed single out leptons of one flavor!
By allowing different leptons to couple differently to Z' bosons, one gets some advantages with respect to simpler universal models: the various experimental results on electroweak precision observables -most notably those coming from the LEP and LEP II experiments- do not constrain just as strictly the existence of this new block of the standard model any more; a simple way to see this is to consider that the initial state of LEP collisions is composed of just leptons of one kind - electrons and positrons. In addition, one gives oneself enough room to speculate on the existence of resonances in the spectrum of electron-positron pairs of high-energy produced at the Tevatron, without having to come to terms with the fact that a similar signal does not occur in the equivalent spectrum of muon pairs.
An excursion into speculand
This is where the paper allows itself a slight excursion into speculative territory: something which I actually consider a good thing, in a world populated with abstruse string theory papers which leave experimentalists out of job. On page 18 they focus on the 240 GeV "signal" that the CDF dielectron analysis "evidences" in its data. I have discussed that fluctuation a few weeks ago, but really, I consider it just another curiosity of present-day results, liable to be washed out by updated results. Nonetheless, the authors demonstrate quite neatly that such a signal is completely compatible with all existing bounds, once one relaxes the universality bound, allowing for a new U(1)' governed by a charge X=B-3L_e, that is one which only depends on electrons, and is insensitive on other leptons.
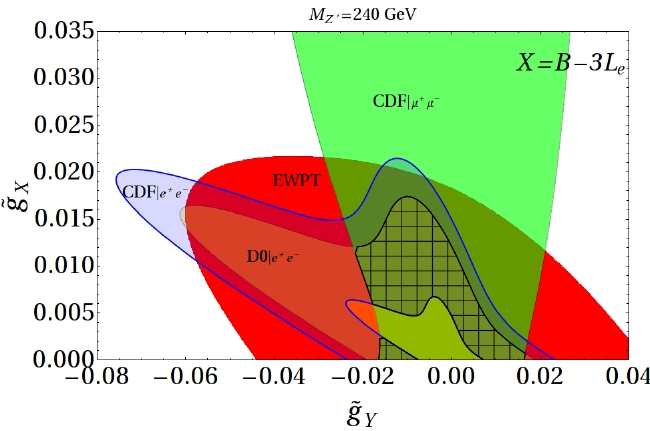
The picture above is quite complicated: it mixes with different colour shading several regions of the parameter space, which are allowed by experimental studies. The plane is spanned by the new couplings introduced by the additional group, g_X and g_Y (Y is still the weak hypercharge, and X is the new charge, X=B-3L_e in this case: a combination using only a non-zero coupling to electrons of the Z' is thus implicit here). Please concentrate on the textured grey region at the center: this region is allowed by all searches, and shows that a 240 Z' boson coupling preferentially to electron pairs is not excluded by present-day experiments: a small but non-zero value of the couplings introduced by the new hypothetical group, in fact, is still possible.
Conclusions
Coming back to the main focus of the study, Salvioni et al. consider several different combinations making up the charge X, and perform careful global fits to all the electroweak data available to distill the information you and me are most interested about: they show which regions of phase space for the masses and couplings of the new Z' bosons resulting from a U(1)' group are left uncovered by present-day bounds. They also explicitly compute the regions of phase space of these models which proton-proton collisions collected in the 2010 running of the LHC will be capable of reach.
Interestingly, the result is that the LHC experiments may indeed have a shot at reaching those phase space points in a very near future. That might not come as a surprise, given that the specific signature of the new U(1)' is a heavy neutral particle, which has exactly the characteristics required to have been hiding above a mass threshold reachable by lower-energy colliders. However, if you remember that electroweak precision tests are powerfully constraining new physics models, you realize why the non-universality of the considered models is the atout that allows us to look with added interest to the data coming out of ATLAS and CMS next year.
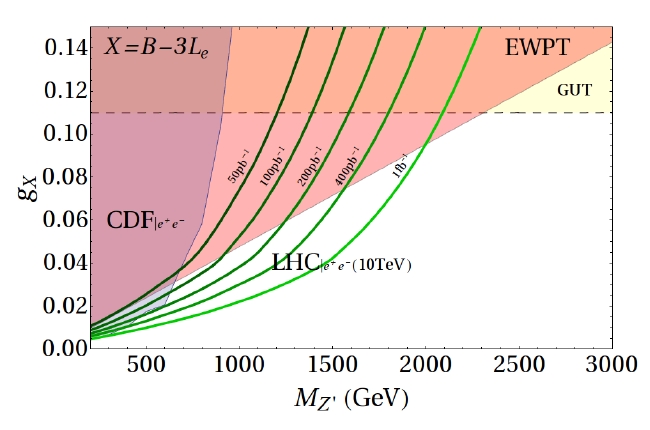
In the figure above you see that for the case of a charge X=B-3L_e the LHC experiments can hardly do much better than the Tevatron's CDF, and that both are fighting mightily with pre-existing constraints from electroweak precision observables (labeled EWPT). The curves delimit regions of the Z' mass and the coupling g_X which can be discovered at a significance of five standard deviations, with LHC running at 10 TeV center-of-mass energy and with different amounts of integrated luminosity. Nothing doing for a while with the LHC if nature has chosen such a U(1)' extension of the standard model!
Instead, with X=B-3L_mu, the picture changes dramatically, as shown below! Now large values of the coupling are still allowed by electroweak data, and one may zoom out in the vertical axis, finding green pastures which LHC experiments can reach even by running at a center-of-mass energy of 7 TeV, and with just 50 inverse picobarns of luminosity.
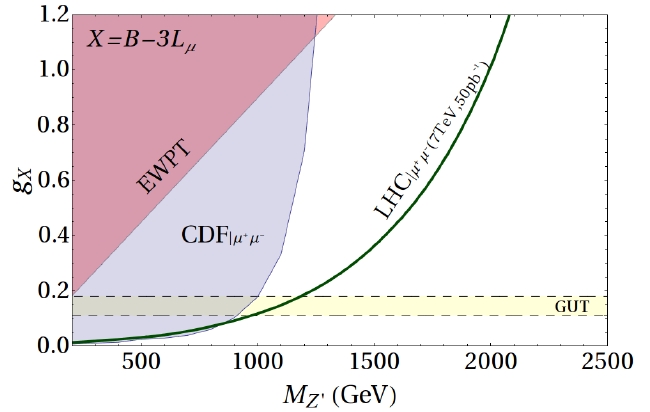
I can only say "good luck, LHC"! And many thanks to Salvioni, Strumia, Villadoro and Zwirner, for giving us something to look forward to in the coming months!





Comments