Perhaps a bit too simple, but certainly appealing. Extensions of the Standard Model which imply the existence of a new U(1) gauge group to complement the SU(2)xU(1) structure of electroweak interactions have been put forth in a number of slightly different versions. All imply the existence of a new Z' boson, a heavier version of the Z0. For those not yet introduced to the latter, the Z0 is the neutral vector boson hypothesized by Glashow, Salam and Weinberg in the sixties to complete a triplet of weak currents and thereby allow the unification of weak and electromagnetic interactions. Its first experimental effect was seen in neutral current interactions observed in 1973 in neutrino bubble chamber detectors, a discovery which convinced everybody of the correctness of the electroweak model; the Z0 was then discovered by Rubbia and collaborators in 1983 with the UA1 detector at CERN when its decays to charged lepton pairs were directly observed.

The Z', like the Z0, should (or should not, in some less straightforward versions of the theory called "leptophobic") decay to pairs of electrons or muons. And the latter particles are very easy to detect and measure with the CMS detector. So it is not a surprise for us to see a very clean spectrum of dilepton invariant masses, extending from below the Z0 mass to multiple TeV. The spectrum, alas, does not show any sign of a second bump besides the towering Z0 peak on the left. Such a bump would be a direct proof of the existence of a Z'. Instead, CMS can only set lower limits on the mass of the particle.

Below can be seen the dimuon (top) and dielectron (bottom) mass distribution measured by CMS (black points) in 4 inverse femtobarns of 2012 data collected at 8 TeV centre-of-mass energy. Expected standard model backgrounds are overlaid with different colours; the Z0 production component (light blue) is the largest. The data agree well with backgrounds, and no Z' signal is observed.




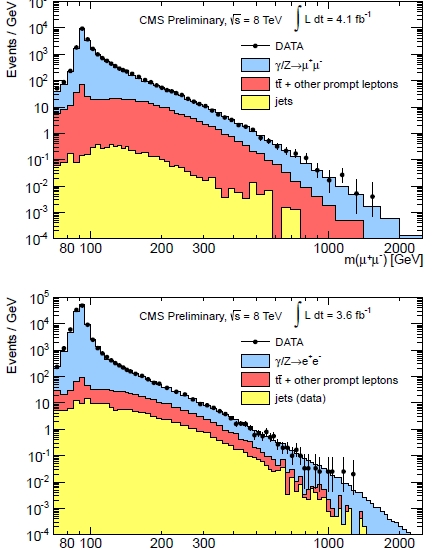
The reasoning, however, is not as simple as one would be tempted to make it by looking at the plots above, "I see no Z' bumps here, up to 2 TeV of mass, so the Z' must have a mass larger than 2 TeV if it exists". That would be silly: one needs to take into account the size of the contribution that a signal would give to the distribution.

What is done, instead, is to place an upper limit on the number of Z' decays that contribute to the data, as a function of the hypothetical Z' mass. So, for instance, having observed one event at a mass of 1300 GeV or so, and expecting to see roughly as much from background sources not related to the exotic Z' production processes, CMS sets an upper limit of a few events (with a statistical procedure which I have discussed elsewhere), if the Z' has a mass of 1300 GeV. Those few events get then converted in the total cross section limit of the new particle production, using the fact that the number of observed events N is related to the signal cross section σ and the detection efficiency ε through the formula N = σ ε L, where L is the integrated luminosity used in the search.

Once the cross section limit is extracted, one compares it with the cross section that a Z' would have, if its mass where of 1300 GeV. If the predicted cross section is larger than the limit obtained by CMS, then a Z' with the quoted mass can be excluded: if it were there, it would have produced an observable excess of events, given detection efficiency and data size.

CMS sets lower limits on a number of different flavours of Z'-producing models. The simplest model is the one which produces a Z' which behaves exactly like a Z0: in that case, the mass limit is at 2590 GeV. The preprint describing the details of the search can be found here.