In good order, below I explain first of all 1) what is CDF, 2) what is the Tevatron, 3) what are Higgs bosons from Supersymmetry, 4) how can these be sought with bottom quarks, and 5) what are bottom quark jets. After I am done with these five explanations, those of you who are still here will no doubt appreciate the results I am showing today. Can I make it in 5 minutes ? Sure, but can you read forty lines of text in the same amount of time ?
Five simple explanations in five minutes of your time
Minute 1 - First of all, CDF. It is arguably the longest-lasting physics experiment in the history of physics, with a project dating back to 1979, and first data collected in 1985. CDF is a general purpose experiment: a 5000-Ton device designed to detect and measure all products of proton-antiproton collisions. It is built like an onion around the interaction point, from which scores of particles created in the collisions fly out at light speed three million times a second. At the core of the onion there are many precise layers of silicon detectors and sensitive wires that record the passage of individual charged particles within a strong magnetic field: from the lining up of many measurement points, the helical trajectories of charged particles bent by the magnet are reconstructed; the bending is inversely proportional to the momenta, so the latter can be determined from the former. Outside, layers of heavy metals interspersed with detecting elements allow to determine the collective behavior of streams of particles, destroying them and measuring their total energy. A picture of CDF during the installation of the silicon detector is shown on the left.
Minute 2 - The CDF experiment collects the results of high-energy interactions produced when protons and antiprotons are accelerated to light speed and then aimed at one another by the Tevatron accelerator at Fermilab (see an aerial picture of the site of the lab on the right). The Tevatron is a synchrotron - it is built with powerful magnets curving the orbit of the particles, alternated with sections where these are increasingly accelerated by electric fields. A synchrony is necessary because as particles increase their energy, magnets need to increase their power accordingly, to keep them on the same curved orbit. After being injected and accelerated, protons and antiprotons are brought to collide at 2 Tera-electronvolt energy, the now second-highest energy available for particle physics studies (7 TeV collisions have started to be produced at CERN ten weeks ago). In such energetic collisions, new states of matter can be produced. Higgs bosons, maybe ?Minute 3 - The Higgs boson is a particle predicted over forty years ago by theorists, to explain the phenomenology of fundamental interactions among elementary particles. A Higgs boson must exist if the Standard Model (SM), our currently accepted theory of nature, is correct. However, at least five different such particles must exist if the world includes not only all the particles we have discovered in the last thirty years, but also a whole new set of bodies with similar properties, a "mirror world" of Supersymmetric (SUSY for insiders) particles. One of these five Higgses, in particular, should be quite similar to the Standard Model one, but it might be produced in larger numbers. So the Tevatron, while still not sensitive enough to detect SM Higgs bosons, might have a shot at discovering a SUSY Higgs!
Minute 4 - One of the ways by which neutral Higgs bosons might be produced in larger numbers than SM ones is by means of "associated production" with bottom quarks. This is because a SUSY Higgs might have a large "coupling" with b's, i.e. attach more readily to those quarks, and would thus be readily radiated by a energetic bottom quark. And not just that: if the b-H coupling is large, then the Higgs prefers to decay to pairs of bottom quarks, too. This makes it convenient to search for events containing at least three independent bottom-quark jets: one or more from the hard collision, and two more from the decay of the Higgs.
Minute 5 - You might not know what a bottom quark is: in that case, look at the picture on the left, which summarizes the elementary particles of nature. Bottom quarks, labeled "b", are the second-heaviest quarks in the collection of six we know. Quarks are the elementary constituents of protons and neutrons, as well as of many other short-lived particles; particles composed of quarks are called hadrons. When an energetic collision between protons creates a bottom quark of high energy, the latter moves away from the collision point by fragmenting into a collimated stream of hadrons. This is what we call a "jet". By measuring jets in the CDF detector, we infer the energy of the originating quark. ... And we are done! It was not so hard, was it ? If you did not know anything about these five things, and you got this down in the reading, please drop me a line and let me know what you found hard to understand, how long you took to read the text above, and whether you considered dropping out. But later. Now we have something better to do - we can try and figure out what CDF did with the data it collected since 2002, and what is the rather surprising result they have obtained.
A hint of Supersymmetric Higgs bosons
The CDF analysis, which is an update of a former search performed with less data, takes events with at least three jets of hadrons, and selects those where all jets contain a signal of having likely originated from a bottom quark. Since the probability that a generic jet is originated by a bottom quark is small -of the order of a few percent-, the requirement kills backgrounds quite effectively.
Bottom-quark jets can be identified thanks to the fact that among the hadrons they originate there is one so-called B hadron: these particles may travel a few millimeters away from the interaction point before decaying, and this crucial fact allows their identification, thanks to precise silicon tracking detectors contained in the core of CDF: several particles can be seen to radiate from the point of decay of the B hadron instead than from the collision point. The point of convergence of these secondary particles is called a "secondary vertex".
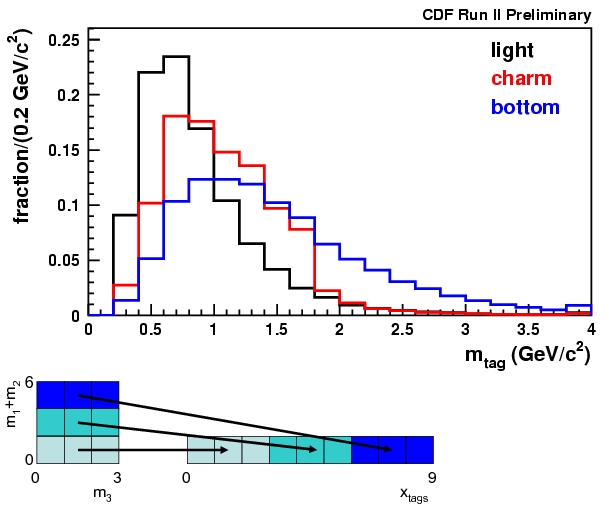
Even after selecting jets wherein a secondary vertex is spotted, one cannot be sure that the jet is a bottom quark one. Lighter quarks may pollute the selection, but there is an additional characteristics that allows a further discrimination: the total mass of the tracks radiating from the vertex. B hadrons are heavy -they weigh over five times more than a whole proton- so they tend to yield much higher total mass. This fact is exploited by the search to discriminate b-quark backgrounds from non-b-quark ones. Below you can see the different vertex mass for jets originated by light quarks (black), charm quarks (in red), and bottom quarks (in blue). Since there are three b-tagged jets, the three values of vertex mass are combined in a single variable "x_tags", as shown in the cartoon below the graph.
A Higgs boson decaying to two b-quarks would produce two energetic jets, but we do not know whic h jets to pick to try and reconstruct the Higgs mass. If we could always choose the two right ones, the resolution on the Higgs mass would help a lot in discriminating it from backgrounds, since backgrounds do not "resonate" -the mass does not show a peak. The analysis makes an educated guess of which jets should come from the Higgs: the two highest-transverse-energy ones. This is a sensible choice, and the resulting resolution on the dijet mass is good enough to provide discrimination from backgrounds. The shape of the invariant mass of the two leading-transverse-energy jets for Higgs bosons of different masses is shown below.
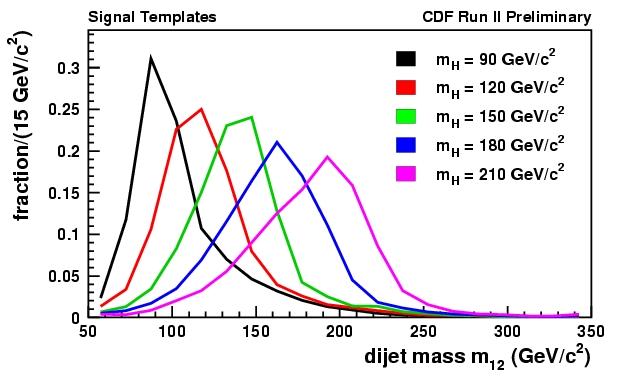
It is clear that the mass resolution is not excellent; however, these distributions are still peaking well enough that they provide the necessary discrimination power with respect to all backgrounds.
In the end, a two-dimensional fit is performed using the vertex mass of b-jet candidates and the dijet mass. Backgrounds are due to quantum chromodynamical processes, whereby two hard jets are produced by the main proton-antiproton collision, and two more are produced by colour radiation. Different combinations of b-quark production processes yield different shapes in the dijet mass distribution, such that attention is required when computing the total expectation from Standard Model proceses. The authors took great care to model the different contributing background shapes, basing their estimates on data with and without secondary vertex tags.
And what are the results ? Results show that the data appears to be well modeled by the sum of backgrounds. However, an even better fit is produced if together with backgrounds, a significant Higgs decay signal is added to the mix! Below you can see the two different ways by which CDF data may be interpreted: the first shows backgrounds alone, the second shows a Higgs contribution, with a 150 GeV mass hypothesized for the supersymmetric particle.
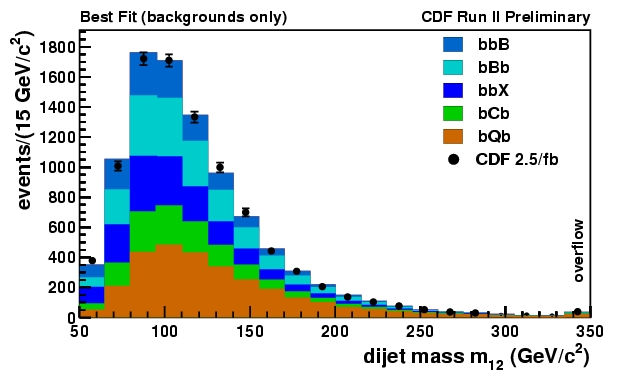
Now, in statistical terms, we have two competing hypotheses, H_0 and H_1, to interpret our data. H_0 is "no Higgs", H_1 is "a Higgs of 150 GeV is present in the data". By comparing the quality of the fit in the two hypotheses, one may derive the significance of the observation -how much do the data "prefer" the H_1 hypothesis. Please note that since H_1 is a nested hypothesis within H_0, H_1 will always fit the data at least as well as H_0: H_1 in fact reverts to H_0 when the assumed number of Higgs candidates is brought to zero. Because of that, the likelihood of the H_1 fit L(H_1) is always larger than the likelihood of the H_0 fit L(H_0).
A simple calculation allows to derive the significance of the Higgs hypothesis from L(H_1)/L(H_0), the ratio of the two likelihood values. The significance appears to exceed slightly 2 standard deviations. Yes, just another two-sigma effect! The standard model has survived much higher-significance claims in the past, and my opinion is that it will survive this one, too. Regardless of our personal bias, the observation is interesting, and the tentative signal requires our attention. We need to improve this search, add more data, and see if those two-sigmas become zero or four!
Below I show one more technical plot produced by the analyzers: the exclusion region of the parameter space of supersymmetry that the search allows. Two of the SUSY parameters are chosen to determine what the data can rule out: a variable called "tangent beta", the tangent of an angle which is related to how strongly the Higgs "couples" to bottom quarks, and the mass of one of the Higgs bosons (the mass of the five Higgs bosons are related to one another, and to plot the data the A Higgs boson is usually chosen as SUSY parameter).
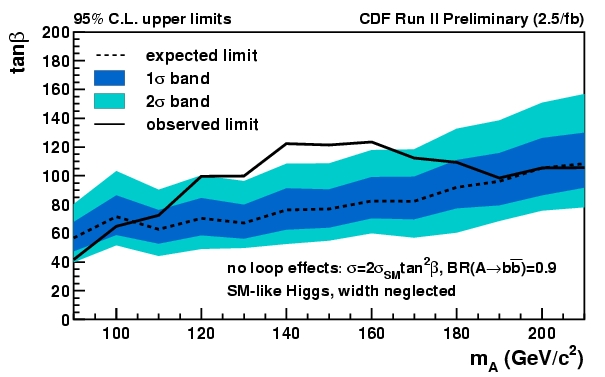
In the exclusion plots, a wide blue band (centered on the hatched limit line) is overlaid to the actual line showing the boundary of the excluded region (excluded values of the parameters lie above the black thick line). The band shows the range of possible exclusion region boundaries that the analysis was expected to produce, at 1-sigma (dark blue) and 2-sigma (light blue). The band gives a feeling of where the data fell -whether it allowed a more stringent limit than expected, or whether it failed to limit the Higgs boson presence in the data. In the CDF analysis a 150 GeV Higgs boson is allowed by the data, and this reflects in the limit being weaker than expected for that value of mass. This is shown clearly by the departure of observed and expected limit for 150 GeV mass.
Comments