And there are dozens of exciting things to study! The excitement is due to the fact that the Standard Model, our very precise theory of elementary particles, produces clear predictions for the way the Higgs boson is produced and the way it decays. So by testing the Higgs boson properties we are also, in a way, searching for new physics hiding in anomalous behaviour of the new found particle.
Higgs decays in the Standard Model
One of the intrinsic properties of a unstable particle is the way it decays. The Higgs, being a particle that "couples" (read: interacts with) to all elementary particles endowed with mass, exhibits an extremely varied and complex pattern of possible decay modes. Below is a short list of Standard Model decays of the Higgs boson, with minimal comments:
- H-->ZZ : this is the "golden" decay mode, the one which provides the cleanest signature experimentally. But it is not the most frequent: out of 100 Higgs bosons, only a few decay this way. If you then consider that in order to reconstruct clearly and without large backgrounds these decays we need to have both Z bosons decay to ee or μμ pairs (the probability of Z-->ee or μμ is 6%), you realize that having the full chain of decays leading to a golden "four-lepton" final state (H->ZZ->eeμμ, for instance) is quite a rare occurrence. CMS and ATLAS have nowadays large signals of the Higgs in this decay mode.
- H-->γγ: this process is even more rare than the one just discussed above. The Higgs does not directly couple to photons, due to the lack of a rest mass of the latter; still, the decay is possible via quantum loops involving W bosons or fermions (most notably the heavy top quark). Only few Higgs bosons out of 1000 decay this way. Both ATLAS and CMS have measured the Higgs production rate precisely with this channel, and also the Higgs mass.
- H-->bb: the decay to a pair of bottom quarks is the most frequent, but it is hard to identify experimentally, because the production of bottom-quark pairs by quantum chromodynamic interactions is a billion times more frequent at the LHC. Nonetheless CMS has already observed a 2-sigma excess of such decays, and the combination of CDF and DZERO experiments at the Tevatron has produced an almost 3-sigma excess. So we know this decay takes place, too.
- H-->ττ: the preference of the Higgs to couple to particles with large mass makes the decay to pairs of tau leptons way more frequent than that to muon or electron pairs. Because of that, the decay to tau pairs has already been observed with large significance, and measurements of production rate and Higgs mass have been published.
- H-->WW: this is the second-highest rate process of decay, but the W bosons can be seen clearly only when they decay to lepton-neutrino pairs, so you have to cope with two neutrinos in the final state, and this prevents you from observing a peak in the invariant mass of the decay products. Still, the excess observed allows precise measurements of the production rate.
- And then there is a number of other decay modes, all precisely predicted in the Standard Model, but which will be harder to extract. To name a few, the H->Zγ decay mode, the H->μμ decay mode, the H->cc. Etcetera.
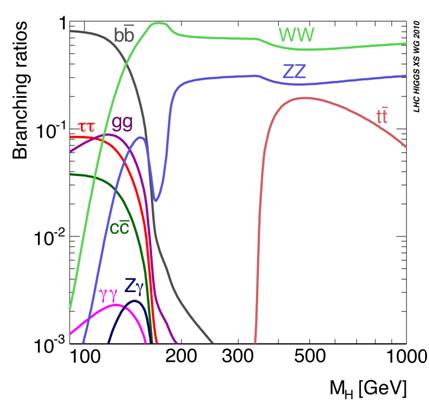A picture which shows the various branching fractions of the Higgs boson, as a function of the Higgs boson mass, is shown on the right. Note that we now know that the Higgs mass is 125.5 GeV (give or take half a GeV), and this implies that some decay modes are practically impossible (e.g. the decay to two top quarks, which collectively weigh 350 GeV - far too much even accepting that they be produced heavily off-mass-shell). It also implies that some decay modes are in principle observable (the H->Zγ one, for instance, would be experimentally too hard if the Higgs weighted, say, 180 GeV).
A new search for Invisible Higgs bosons
So, after the above introduction, I can finally mention the recent pubished search performed by the CMS experiment for invisible Higgs bosons. What does it mean, invisible ? It means that we can conceive the possibility that, in some extension of the Standard Model, a significant part of the produced Higgs bosons decay to invisible particles. An invisible particle is just one particle which does not interact, or does so very weakly, with ordinary matter. Neutrinos are prime examples of particles we know to exist which are exhibiting that kind of behaviour: for instance, W bosons are known to decay two ninths of the time into electron-neutrino or muon-neutrino pairs, and we precisely reconstruct these decays although we cannot detect the neutrinos in the detectors. We do so by measuring "by subtraction" the missing momentum that neutrinos carry away. Let me explain.
Imagine you and a friend play pool and you simultaneously aim your balls at one another from two sides of the table. The two balls travel on a straight path and they collide at the center of the table. You can hardly predict the trajectory of the balls after they meet, since it depends on their spin, their relative speeds, the impact parameter (how perfect is the alignment in their trajectories, that is). What you would be very surprised to observe, though, would be the balls both traveling out of the collision points toward your right, or toward your left. They would appear to be recoiling about something invisible.
The law of conservation of momentum in the considered case describes the effect of the absence of any net force acting on the balls in the direction transverse to their original direction: if a ball is pushed toward the right by the collision with the other ball, the other ball must feel an equal force pushing it toward the left. Under no circumstance can both balls be pushed to the right, or both to the left, since there is no agent in the system which is performing that task: the pool table is inert - it just "sustains" the balls against their gravitational force.
If you understood the example, you would be just as surprised now if I showed you a particle collision where two protons travel on a straight line one against the other at the speed of light, and all the debris they produce in their collision were observed to flow out in direction orthogonal to the beam after the collision. There is only one explanation for such an effect: something invisible is being emitted in the opposite direction in the transverse plane, such that its momentum vector balances the sum of the other ones.
This concept is used routinely in hadron collisions to measure the momentum of the neutrino emitted in a W boson decay to lepton-neutrino pair. Note that you cannot infer the component of the momentum in the direction longitudinal to the beam, because there is no knowledge of the longitudinal momentum carried by the quarks in the initial state; only the fact that their transverse momentum is close to zero is well known.
CMS sought for invisible Higgs bosons using the predicted topology of events producing the Higgs together with two energetic forward hadronic jets. Such events arise in the so-called "vector-boson fusion" mechanism: quarks from the initial protons "radiate" W or Z bosons which fuse together to create the Higgs. The quarks after the boson emission recoil in the transverse direction, creating two energetic jets with typically a small angle with respect to the beams direction.
Of course we do not expect to observe a signal of invisible Higgs bosons in the Standard Model: the Higgs must have a really, really tiny coupling to neutrinos, such that its decay H-->νν is absolutely unobservable and irrelevant. However, a heavy particle with weak interactions only could couple to the Higgs significantly, and we would then be able to see such a process by observing an excess of events with two forward energetic jets and a significant amount of missing transverse energy above known backgrounds.
After a cut selecting events with non-back-to-back hadronic jets, the dominant backgrounds are produced by real sources of missing transverse energy: neutrinos, that is. The Z boson may decay to two neutrinos (it does so 20% of the time) and be produced together with energetic jets, so that process needs to be accounted for in detail. Fortunately, we can pinpoint it by looking at the Z->ee and Z->μμ decays we collect in our data, which exhibit the same kind of kinematics. By acting as if we did not measure the leptons in these events, we have a precise model of the missing transverse energy that the corresponding Z->νν + jets events produce.
Another background is due to production of W bosons decaying leptonically, where the lepton (e, μ, or τ) is not detected. This background can also be well studied with the data when the lepton is observed as it should.
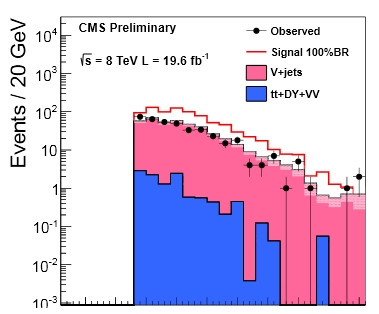
In the end, the search finds no excess of invisible Higgs decays. The "money plot" is shown above: it is a missing transverse energy distribution, where data (black points) and backgrounds (full histograms stacked) are in agreement, while a significant contribution from invisible Higgs decays (extra empty histogram, in red) would shift the data up. Using that, an upper limit can be set on the branching fraction, assuming that the production occurs at the SM predicted rate. The result is that the invisible branching fraction is smaller than 69%, at 95% confidence level.
In conclusion, the Higgs boson is observed where we should see it - in WW pairs, ZZ pairs, tau lepton pairs, photon pairs, b-quark pairs - and not observed in any other decay mode, where we should not see it according to our present understanding of subnuclear physics. A decay with large branching fraction to a pair of neutralinos, for instance, would have been observed by the analysis reported here.
For more detail of this nice new CMS result please read the paper !
Comments