1) Grandma dreams of her deceased husband spelling a sequence of numbers, and the following day she sees the same sequence coming out at Lotto. Was grandpa trying to let her win a large sum ? It will be quite hard to convince her otherwise.
2) You wish a horrible death to a guy who fails to yield at an intersection, and a few miles down the road you drive by his wrecked car in flames. Supernatural powers ?
3) A nurse claims that the moon causes a unusually large number of births: every time there is a really busy night at the delivery room, she watches out of the window and sees a full moon. An astral influence ?
4) You visit a remote foreign country for the first time, and bump into your old friend Seymour, whom you had not seen in decades. Destiny ? Whatever it is, this freaks you out, n'est ce pas ?
The logical explanations
Granted that complete chance is always a possible answer, there are usually logical explanations to those unlikely occurrences, and they can be ascribed to different effects:
1) Grandma listened those numbers spelt on the radio in the morning while she was distracted, and involuntarily merged that memory with that of a dream of her husband, which she had the night before. Seeing the same numbers in the newspaper in the afternoon startles her: the effect is involuntarily made up by her declining mental faculties.
2) The guy you cursed on the road was totally drunk, and his reckless driving was the cause of both your curse and his accident. Among all the drivers that elicit your cursing, the fraction of drunk drivers is very high, and the latter have a much higher chance of causing accidents: this explains the apparent mysterious powers of your death wish.
3) The nurse watches out of the window every time there is a unusually large number of births, and she more easily records in her mind the "positive reinforcements" of her theory. When there indeed is a close-to-full moon she will get a kick out of it and she will remember that night much better than all those when she looked out and saw no moon or just a slice of it. After a couple of years of practice, nothing will shake her confidence that the moon influences the date of delivery, although her "evidence" is entirely based on biasing herself into picking the successes in a random sequence of trials.The three cases above highlight different mechanisms through which a "unbelievable coincidence" may arise in our everyday life: the coincidence may be a fake -intentional or not- as the one due to grandma's poor memory; it may be a hidden correlation between two apparently random variables, one of which "selects" the other, as in the case of the drunk driver; or it may be due to our selective memory, as it happens to the nurse in the example above. Fake, Correlation, and Bias are the three tags of the effects at work, in the cases we have considered this far.
The Look-Elsewhere Effect
The fourth case, however, deserves a different discussion. Upon meeting Seymour, you cannot invoke any of the above effects to mitigate the significance of your observation: you are damn sure it was him, since you even ended up sharing a beer and talking about ye good ole times -no fake; you have no reason to believe he followed you, nor are you in that remote bit of land for the same reason that he is (as might happen if you have a common profession and you are there for the same reason) -no correlation; and this is a single event, since you either met an old friend or not in your trip: no selection bias. Or not so ?
In fact, a selection bias is indeed present, but as is often the case with similar problems, in order to see it you must observe the system from outside. You visited many unfamiliar places in your trip on that occasion; and in general, you travel a lot. Moreover, you would have been just as surprised to meet a famous person, like a well-known actor, or a politician, as you were to find Seymour. So indeed, the question "How likely it may be that upon visiting this remote land for the first time in my life, I meet a good, old friend ?" is very, very ill-posed. You had even forgotten of Seymour, and now you talk as if he is a very important person in your life!
The right question to ask would instead be "How likely it is that, in the last twenty years of my travel, I ended up meeting a person I knew, either personally or from newspapers or TV, in a remote place far from where we both live or work?", and this must be a one-in-ten sort of probability, not a one-in-a-million like the previous question would suggest! By loosening the net, and by throwing it several times, your chance to catch even just one fish increases enormously.
The mechanism at work -the negligence of the universe of possibilities that could have yielded a similarly cataloged event- is quite common, and quite relevant for scientific investigations at least as much as it is to model the chance of a cheerful rendez-vous. It is called "look-elsewhere effect". One way of thinking at this effect is that it arises when one focuses on characteristics of the observed phenomenon which are inessential.
And in particle physics...
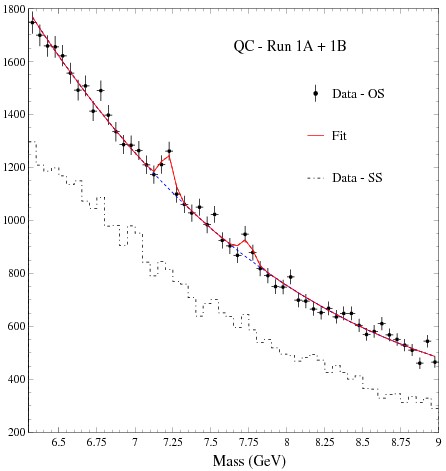The look-elsewhere effect is very common in physics searches for uncommon events. It is present in all searches for new particles, for instance. A new particle may be discovered by reconstructing its mass from the measured energy and flight direction of all its decay products. Take as an example the mass spectrum shown on the right, which is constructed by taking events containing two opposite-charge muons recorded by the CDF detector at the Tevatron proton-antiproton collider, in its 1994-1995 run. You measure the muons, compute their total mass, and draw its distribution (the black points with error bars). Then you ask yourself the question: "Do I see a bell-shaped bump (a Gaussian) in this smoothly falling distribution ?". (The curve actually shows two hypothetical bumps, but leave this detail alone now.)Indeed, a bump seems to be there, at a mass of about 7.2 GeV. If one tries to fit the bump and the smooth background with a suitable functional form, one obtains the continuous line, and by comparing the parameters of that signal-plus-background fit to the parameters of an alternative background-only fit one can compute the "significance" of such a signal of a hypothetical 7.2 GeV particle, using a quite well-known statistical formula (but one which even large experiments sometimes manage to use improperly, obtaining incorrect results). However, the answer one gets from that statistical formula does not account for the fact that the bump may have appeared anywhere in the spectrum we examined. Look-elsewhere warning! Whether due to a Gaussian-shape fluctuation of background processes or to a few genuine decays of a so-far-unknown exotic particle, the bump would have been taken just as seriously if it had happened at 7.0, or 8.0 GeV, or anywhere else in the examined spectrum.
Physicists use the p-value of an observation to classify its significance. A p-value is the computed probability of the effect. In the case of a unknown-mass particle signal, the p-value resulting from the statistical test must be multiplied by the number of places in the spectrum where it might have been spotted (this is a rule of thumb, but it gets close to the right answer, which requires more accurate studies to be obtained). This factor equates to roughly the width of the mass interval considered in the histogram, divided by the width of the particle signal (we imagine that the signal must have a width compatible to the experimental mass resolution in order to be taken seriously, in this particular case; otherwise, some accounting for a unknown width must also be made). In the case at hand, the probability of the Gaussian bump gets multiplied by at least a factor 20, and an effect having an apparent significance of almost four standard deviations is therefore correctly interpreted as one corresponding to little more than two standard deviations.
A similar case is discussed in my recent paper on the Omega_b observation (see here for a post about it). There, the CDF and D0 collaboration both failed to fully account for the effect. Or to be precise, CDF did it partly: since they claimed they accounted for the look-elsewhere effect within the mass region where they expected to observe the Omega_b signal (which, after all, was a well-predicted state, whose mass had to lie in the quoted interval); D0, on the other hand, ended up fitting a signal outside of that interval, but in their publication they neglected the tenfold increase in probability of a background fluctuation due to the look-elsewhere effect.
D0 did come clean, after my paper appeared on the arxiv. A few days ago they revised their "frequently asked questions" web page, where they admit that the significance gets decreased (according to them just by a factor of 7, though) if one accounts for the look-elsewhere effect, which I had estimated in my paper. Unfortunately, they still have not answered my other question on the way they use the p-value formula. I guess it does not matter much in the end: 5-sigma, 4.6-sigma... It does not make much difference: the Omega_b exists, it has been discovered by D0, and the mass has been measured well by CDF one year afterwards. End of the story, for me.
Comments