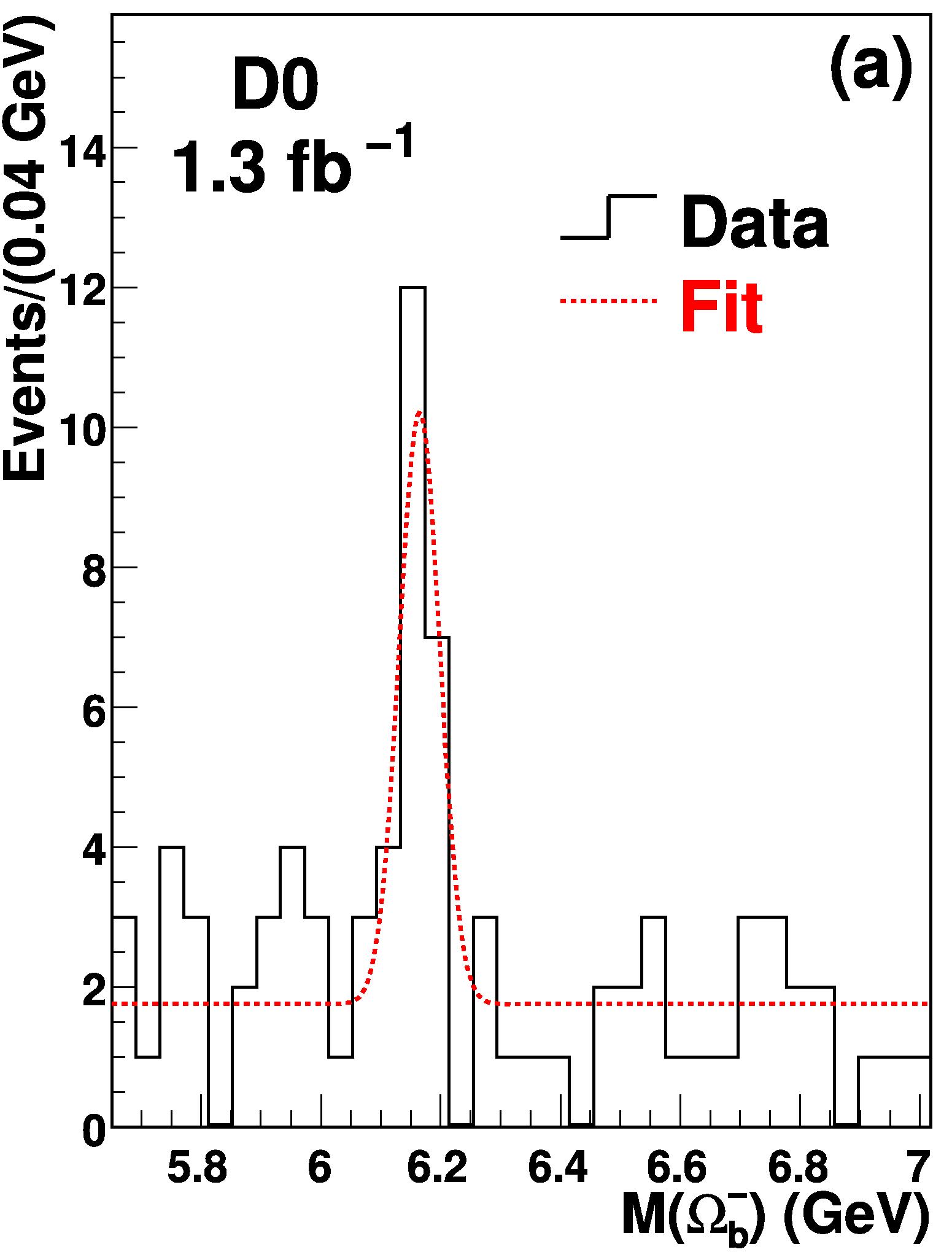
Last May the CDF collaboration published their observation of the  baryon, a particle made by a very exotic "bss" quark triplet. The CDF result came almost one year after a similar measurement was published by the competitor experiment, D0. D0 had claimed first observation of the  in 2008, with a signal whose statistical significance was quoted at 5.4 standard deviations -an effect which, if due to a background fluctuation, has a probability of occurrence of merely 67 times in a billion. The D0 peak is shown on the right, with a fit overlaid.

The two observations led me to investigate the matter, because the mass measurements of this new baryon quoted by CDF and D0 were in startling disagreement with each other: CDF quoted , while D0 quoted . These numbers, taken at face value, disagree by over 6 standard deviations! Were the two new states found by CDF and D0 the same particle or not ?

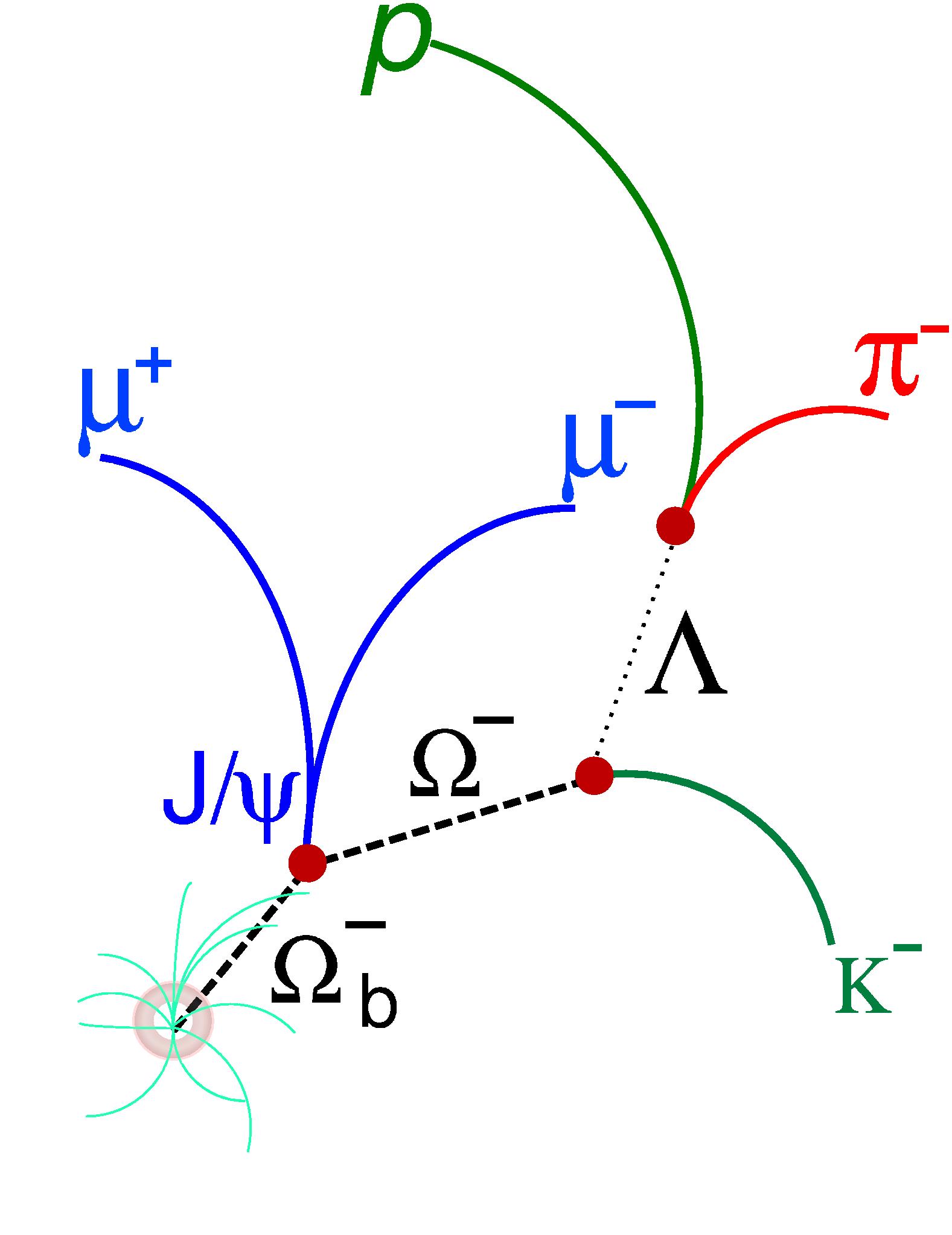They certainly are. The  decay produces a chain reaction which is one of the most striking signatures you might think of, as far as weak decays go (see a sketch on the right, courtesy D0 again: in it you see the Omega_b produced at the bottom left decay into a J/psi meson and a Omega^- baryon; the former immediately materializes two muons, the latter continues the cascade into a Lambda and finally a proton). Indeed, its lower-mass brother, the Omega, was discovered in 1964 thanks to a single photographic plate -one event, one discovery! The distinctive nature of the decay chain is so unmistakable that it is really, really tough to claim that either CDF and D0 saw anything different. And on the other hand, the significances quoted by the two experiments easily surpass the coveted mark of "five standard deviations" which puts them above any suspicion of a background fluctuation. Or do they ?

I decided to check the numbers provided by the two experiments, and in so doing I discovered that D0 had made a mistake in their computation: they evaluated the significance from a delta-log-likelihood value (the difference between two numbers obtained by fitting for the resonance or for the background alone) by assuming this difference came from adding to the fit one degree of freedom, instead of the two which they had left floating (mass and signal yield). Using the correct number of degrees of freedom, the probability rose by a factor 6.4, from 67 in a billion to 430 in a billion. Still rather improbable, duh! I agree -but when it comes to numbers in scientific publication, one expects them to be correct.

By doing pseudoexperiments, I also discovered that if a trials factor was included in the calculation, those 430 times in a billion rose tenfold, to 4.1 in a million: still improbable, but not terribly so any more!

(By the way, a trials factor is a multiplicative factor to be applied on the computed probability of an effect: the factor accounts for the way the effect was unearthed, and corrects the probability estimate; I wrote about this recently here, giving some real-life examples. The trials factor is also called "look-elsewhere effect": in physics, when we go bump-hunting in a particle mass spectrum, we know that the wider is our search region, the easier it is that we get tricked into seeing a signal when in fact we are staring at a background fluctuation.)

After doing my homework, I tried to figure out whether there was more material available than the published paper, and found a "Frequently Asked Questions" in the D0 web page of the Omega_b observation. In it, through the first week of October (before I submitted my preprint to the arxiv) you could read the following statement:

"What we report is purely the statistical significance based on the ratio of likelihoods under the signal-plus-background and background-only hypotheses. Therefore, no systematic uncertainties are included, although we have verified that, after all systematic variations on the analysis, the significance always remains above five standard deviations. Our estimate of the significance does also not include a trials factor. We believe this is not necessary since we have a specific final state (with well-known mass resolution) and a fairly narrow mass window (5.6-7.0 GeV) where we are searching for this particle. [...]"

I was startled to read that D0 did not consider useful to include a trials factor in their significance calculation. But I also had to note the absence of any mention of the mistake in the computation of the significance, due to the use of only one degree of freedom: this let down my hope that, after the publication of the article, they had realized the problem of their significance calculation.

I thus wrote privately to the D0 physics conveners, mentioning that I was putting together an article where I discussed the two observations, and pointing out the mistake. Unfortunately, I received no answer. After waiting a couple of weeks, I submitted my paper to the Cornell Arxiv. Despite the lack of an answer, I found out soon that my investigations on the D0 Omega_b significance had had an effect: the "frequently asked questions" web page available at the D0 web site had been modified in the meantime.

The page now explained that the inclusion of a "trials factor" would derate from 5.4 to 5.05 standard deviations the significance of their signal. Still, there was no mention of the use of one degree of freedom for the evaluation of these numbers! A striking instance of perseverare diabolicum.

Let us fast-forward one month. Today I am about to submit my preprint on the Omega_b mass controversy for publication to a scientific journal. I like to check my sources, and since in my article I am quoting the D0 FAQ web page, I decided to give it a last look. Lo and behold, the page has changed again! They are now at version 1.9 of the document, and the version presently online is dated November 8th, 2009. Here is the latest version of the answer in question:

"What we report is purely the statistical significance based on the ratio of likelihoods under the signal-plus-background and background-only hypotheses. The significance of 5.4 standard deviations quoted in the published Phys. Rev. Lett article is reduced to 5.05 standard deviations once a trials factor is included allowing for the test mass of the two-body final state (J/psi+Omega) to lie in the 5.6-7.0 GeV mass region where we are searching for this particle.[...] The significance of the observed signal with an optimized event selection where the transverse momentum requirement on the Omega_b candidate was increased from 6 to 7 GeV is 5.8 standard deviation taking into account the trial factor".

I was not smart enough to save the previous instance of the document, so I cannot really compare the present one above to the one appeared just after the publication of my preprint (I have saved the present one, though -erro sed non persevero!). I however believe, based on my admittedly scarce memory, that the new modification is an added sentence, where they now say that the significance of the signal rises to 5.8 standard deviations if an optimized selection is applied by a tighter cut on the Omega_b transverse momentum (passing from 6 to 7 GeV). Again, no mention of the degrees of freedom issue. This is rather annoying!

Leaving aside the issue of trials factor and degrees of freedom, there is something else to say about this "optimized selection", if one wants to be picky. Let us read what they write in their original 2008 publication:

"To further enhance the Omega^- signal over the combinatorial background, kinematic variables associated with daughter particle momenta, vertices, and track qualities are combined using boosted decision trees (BDT)[10,11]. .... The BDT selection retains 87% of the Omega^- signal while rejecting 89% of the background."

So they did optimize with advanced multivariate tools their Omega^- signal, which is one of the decay products of the Omega_b. For the latter, instead, they appeared to not do an optimized selection. A few lines down we read, in fact:

"To select Omega_b \to J/\psi \Omega" candidates, we develop selection criteria using the MC Omega_b events as the signal and the data wrong-sign events as the background [...] and impose a minimum Pt cut of 6 GeV on the Omega_b candidates."

My question is the following: is it fair to have a data selection which evidences a new resonance, which has been studied -optimized or not- to discover that state; publish the observation; and then go back and fiddle with the selection cuts, in order to write in a FAQ page that the significance of the signal rises from 5.05 to 5.8 standard deviations if "the pT requirement is increased" ?

Maybe the answer is: Yes, it is fair, but it is not scientifically compelling. Because the nature of the quantity we are discussing, statistical significance, is delicate. The failure to take an a-priori stand and the tweaking of the selection cuts is bound to make "significance" a worthless quantity.