A Sunday morning browsing through preprints recently posted in the Cornell Arxiv revealed interesting reading material. If you have a couple of hours to kill next week, why not having a look at the following papers ? It will definitely hurt you less than spending the time on your WII or watching Jerry Springer.

- Alejandro Rivero, "Unbroken Supersymmetry Without New Particles", 0910.4793: Alejandro is a friend and he already wrote in this blog about his "sbootstrap" theory. To tell you in two words what this is about, he moves from a startling numerical coincidence between the masses of charged leptons (the Koide' mass formula) to hypothesize that the role of Supersymmetrical particles in the Standard Model is taken by composite mesons. It is a bold speculation, and it is certainly worth ten minutes of your time, if you can read English and know the basics of group theory.

- Gautam Bhattacharyya, "A Pedagogical Review of Electroweak Symmetry Breaking Scenarios", 0910.5095: a quite well-written and comprehensive summary of the theory of electroweak symmetry breaking in the standard model, with explanations of models involving little Higgs or Higgless breakings. I found it a very useful resource, especially for experimentalists wishing to refresh their memory; but beware, the math is only as simple as possible, not simpler.

- Tilman Plehn, Gavin Salam, Michael Spannowsky, "Fat Jets for a Light Higgs", 0910.5472: a recipe for looking for the Higgs boson at the LHC, using the associated production for low Higgs boson masses and "fat jets" plus triple b-tagging. The study is interesting, although I was rather puzzled to learn that "After long debates this signature has recently been abandoned by both LHC experiments". The authors quote as evidence for this claim the observation that the signature has been recently removed from the standard Higgs "discovery reach" plots of ATLAS and CMS, but I would like to remind them that this is a necessary, but not a sufficient, condition for what they claim. In fact, my group is still pursuing that signature, with a new technique. Since 30 to 100 inverse femtobarns of data are needed, however, it is clearly something on which we are taking our time...

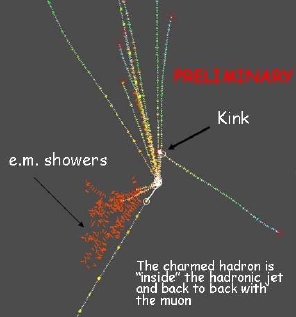- H. Pessard, "Status of the OPERA Neutrino Experiment", 0910.5701: a short review of the status of OPERA, a really cool experiment which aims to detect oscillations of muon neutrinos (from a CERN beam shot underground in the direction of the Gran Sasso underground facility) into tau neutrinos. Tau neutrinos are notoriously hard to detect: technically it is the last standard model fermion to have been directly discovered, although nobody could really doubt of their existence after the tau lepton discovery and the LEP measurement of the Z boson width. OPERA uses photographic emulsions to reach micrometric precision in the tracking of charged particles emitted when tau neutrinos hit nuclei, produce tau leptons, and the latter decays after a path of few microns in the emulsion. Have a look at a typical picture (this one shows acharmed meson decay though) on the right.
I think OPERA is cool because of its concept: bricks of emulsions where neutrino interactions are captured get removed from the detector progressively, and analyzed as data taking proceeds. It reminds me of HAL, the supercomputer in "2001, the Space Odyssey", being disassembled bit by bit by the vindictive astronaut the machine had tried to kill. For a previous account of OPERA, read here.