In his recent blog post "The World Is Not Woven From Real Stuff", Sascha Vongehr wrote:
Some merely claim that we need quantum mechanics so that the electron does not fall into the atom’s nucleus. Any classical electric charge would spiral into the atom's nucleus. The material that they make up would collapse.... Well, how convincing is this argument? Does it convince you? It would not convince me without a severe dose of already knowing at least a bunch of electromagnetism. Why could there not be some other, more intuitive explanation of why atoms do not collapse?
What I offer in this post is another, more intuitive explanation of why atoms do not collapse.

One of the failures of classical physics, which led to the creation of a then entirely new physics, was its inability to account for the stability of matter. Part of the solution came in 1926, in the form of Heisenberg's uncertainty relation for position and momentum. (Heisenberg himself used the term Unschärfe, which literally means fuzziness.) Part of the problem was how an atom, made up of a few particles, each virtually or literally occupying no space at all, comes to occupy as much space as it does (roughly a tenth of a nanometer across).

The following image illustrates the fuzzy position of the electron relative to the nucleus (a proton) in the ground state of atomic hydrogen. Although the proton is assumed to be at the center, neither it nor the electron is shown. What you see is a cross-section through the center of a spherically symmetric cloud, whose density falls of exponentially. If you integrate this density over a region of space somewhere inside the cloud, you get the probability of finding the electron inside that region, provided the appropriate measurement is made.
ground state of atomic hydrogen
It seems clear enough that the fuzziness of the electron's position (relative to the nucleus) can be at least partly responsible for the space that an atom of hydrogen occupies. But being fuzzy is not enough. The electron's position must also stay fuzzy, and that is where the fuzziness of the electron's momentum (relative to the proton) comes in.

A convenient measure of the fuzziness of the electron's position is the standard deviation Δr of the radial component of the electron's position. If the electrostatic attraction between the electron and the proton were the only force at work, it would cause a decrease in Δr, and the atom would collapse as a result. The stability of the atom requires that the electrostatic attraction be counterbalanced by an effective repulsion. The following images illustrate how this effective repulsion is realized by the fuzziness of the electron's momentum.



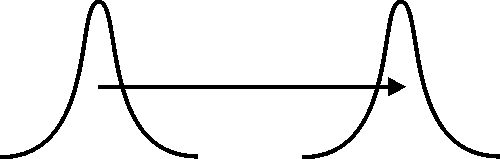
In both images (above and below) we see the fuzzy position of a particle at an earlier and at a later time. Each position is represented by a plot of the corresponding probability distribution, and the particle's momentum is indicated by a horizontal arrow. In the image above, we assume that the momentum is sharp, so that the fuzziness of the particle's position (indicated by the widths of the plots) remains unchanged. In the image below, the particle's momentum is fuzzy, and the fuzziness of its position increases as a result. Invoking the classical relation of proportionality between momentum and velocity, we may say that the fuzziness of the position of a particle moving with a fuzzy velocity increases with time.



So the electrostatic attraction between the electron and the proton tends to decrease Δr, while the electron's fuzzy momentum relative to the proton tends to increase Δr. With both tendencies present, equilibrium is possible.

But a stable equilibrium requires more. If the mean distance between the two particles decreases, their electrostatic attraction increases. A stable equilibrium is possible only if the effective repulsion increases at the same time. We can therefore expect that a decrease in
Δr is accompanied by an increase in Δp, the standard deviation of the radial component of the electron's momentum. The stability of the atom thus requires that the product
ΔrΔp has a positive lower limit, as dictated by Heisenberg's uncertainty principle.

Postscript dated October 9, 2012:
I just revisited this post and noticed with some chagrin that my response to Sascha was rather inadequate. Sascha was of course right in pointing to the time symmetry of the Schrödinger equation, which implies that the later (wider) probability distribution could as well be the earlier one. What I have shown, therefore, is not that the fuzziness of the particle's momentum causes the fuzziness of its position to increase, but merely that the former fuzziness can cause the latter to increase with time. But this is sufficient for the argument I wanted to make.

Sascha thinks that my aim was "to derive fundamental uncertainty." It was not. Taking the fuzziness of the particle's position for granted, my aim was to show how the uncertainty relation accounts for the atom's stability. Having shown that the fuzziness of momentum can cause the fuzziness of position to increase, and thus can counterbalance the effect of the electrostatic attraction, I assume that this is what it does. I then ask, what does it take for the equilibrium between the two effects to be stable? What I find is that the product of Δr and Δp must have a positive lower limit, precisely as mandated by the uncertainty principle.