In standard Cosmology, the matter energy density cannot accelerate the expansion of the Universe. This is basically due to its too fast decrease as a function of the cosmic time t (age of the Universe) and of the cosmic scale factor a . But the situation can radically change if this decrease is slowed by extra energy released in the cosmic expansion of the physical vacuum. This is the subject of the article I uploaded to Research Gate on April 26:
Can matter accelerate the expansion of the Universe? (I)
Luis Gonzalez-Mestres
Abstract - To the present uncertainties of cosmological measurements, theoretical uncertainties should be added and their potential implications carefully explored. A significant example is provided by the possibility that the expanding cosmological vacuum releases energy in the form of standard matter and dark matter, thus modifying the dependence of the matter energy density with respect to the age and size of our Universe. In this case, if the matter energy density decreases more slowly than in standard cosmological patterns, it can naturally be at the origin of the observed acceleration of the expansion of the Universe without any need for dark energy and a cosmological constant. We illustrate this possible situation using the cosmology based on the spinorial space-time (SST) we introduced in 1996-97. Other scenarios leading to the same effect at the cosmic level are also briefly discussed. (Part I of a contribution to the ICNFP 2016 Conference, July 2016)
(end of the abstract)To illustrate the mechanism, the article uses in particular the cosmic spinorial space-time already described in several articles of this blog. A specific property of such a cosmology is the presence, in the Friedmann-like equation for H2 (the square of the Lundmark-Lemaître-Hubble constant, usually called the Hubble constant, H), of a positive term t-2 associated to the cosmic SST curvature. This term turns out to help the new phenomenon considered. A simplied version of the Friedmann-like equation can then be of the form:
H2 = t-2 + Γ
which corresponds to the equation (3) cited below, Γ being the sum of the term associated to the matter energy density and a possible new version of the cosmological constant. In what follows, we assume that Γ is dominated by the matter energy density.
Then, the possible situation where the matter energy density decreases more slowly as a function of a and t than in standard cosmological patterns is dealt with as follows in my article:
(...)
If the physical vacuum has a nontrivial internal structure, this structure is sensitive to the expansion of the Universe where vacuum expands like space and its internal structure must follow this cosmic process. It seems then reasonable to expect that "creating more vacuum" should in principle have a nontrivial cost in energy. This cost can be positive or negative and remains by now unknown, but in any case it does not prevent the space from expanding. In this respect, we assume here that:
- The physical vacuum releases a positive amount of energy as it expands with the present Universe evolution.
- This energy is converted into matter (standard and dark).
- As a consequence, the cosmic matter energy density decreases more slowly than usually expected as the Universe expands.
Then, if Γ corresponds basically to the matter density, its new dependence on the age and size of the Universe can lead to nontrivial effects and, in particular, make unnecessary the usual role of dark energy and the cosmological constant. A simple way to illustrate the basic mechanism can be to write for equation (3):
Γ = γ t-2 (4)
where γ is a constant, and
H2 = t-2 (1 + γ) (5)
where it has been assumed that the matter energy density varies like t-2. One then gets, using the equation H = a-1 da/dt where a is the usual cosmic distance scale:
da/a = (1 + γ)1/2 dt/t (6)
leading to:
a = f tλ (7)
where f is a constant and λ = (1 + γ)1/2, and subsequently to:
d2a/dt2 = λ (λ -1) tλ-2 (8)
Therefore, the expansion of the Universe is accelerated for all positive values of γ without any need for a standard cosmological constant. A positive matter energy density varying like t-2 is enough to produce such an effect.
Writing, as usual, for the standard deceleration parameter q0 :
q0 = - a d2a/dt2 (da/dt)-2 (9)
one gets the value q0 = -0:55 for γ
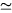1 , i.e. Γ 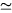t-2 (matter energy term 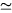SST term).4.1. Other scenarios involving the SST
In the previous example, the limit H t → 1 is replaced by H t → (1 + γ)1/2 with (1 + γ)1/2
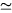√2 for Γ 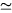t-2 . The relation between H and t is then significantly modified with respect to conventional cosmology or to standard SST predictions.There is, however, no experimental evidence against equations (4)-(5).
The limit H t → 1 would be preserved,simultaneously to the positive sign of d2a/dt2 (positive acceleration), replacing equation (4) by a similar law:
Γ = γ' t-α (10)
where γ' is a constant and 2 < α < 3 . The value α = 3 is a limiting case, where one gets:
H2 = t-2 + γ' t-3 (11)
with a vanishing acceleration at the first order for small t-1. For higher values of α , the acceleration becomes negative at small t-1.
Thus, a matter energy density of the form (10) with 2 < α < 3 : i) preserve the H t → 1 limit at large t ; ii) generate the observed acceleration of the Universe expansion, with a suitable value of γ' .
(end of the extract of my article)
The full text of the article is available at the address http://www.science20.com/uploads/939493515-505753807.pdf
The standard curvature term is not explicitly considered, as it is significantly smaller than the SST curvature term t-2 . But the phenomenon described can also exist with other space-time geometries, including the standard one based on general relativity.
Luis Gonzalez-Mestres
Comments