If you are like me and my friends, there is nothing you enjoy more than sitting around during half-time of the Steelers game and arguing over Maxwell's Demon - the many ways to violate the Second Law of Thermodynamics, namely that heat transfer happens, from warmer to colder, until equilibrium is reached. If I put an ice pack next to Ben Roethlisberger's blazing hot 145 third down QBR (Total Quarterback Rating), for example, the ice pack will not cool down, it will warm up. So it has always been, so shall it must be. It is common sense.
But Maxwell's Demon turns us all into circular reasoning dolts. If we allow James Clerk Maxwell's pesky demonic sprite to run free, letting faster molecules in and out of doors and ruining equilbrium, we end up with perpetual motion machines and the Broncos winning in the playoffs and other craziness. Statisticians love the entropy of the Second Law of Thermodynamics so if you release the Demon, they start taunting you with how great a team the Cleveland Browns are. We don't want that to happen.
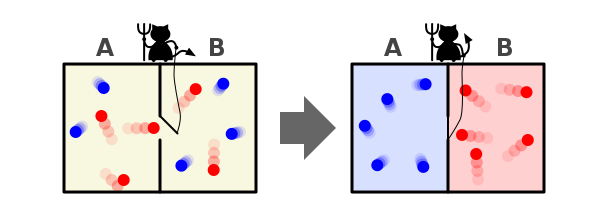
Does this look like a football play? Maxwell came up with this paradox long before the game was invented, so you see where Americans got the idea for X's and O's - they were slow and fast-vibrating molecules, which meant more heat.
But Maxwell's Demon is not the only paradox worth debating over an Iron City beer, there are lots of others known to lots of people. The Monty Hall paradox, for example, deals with conditional probability. It was based on a game show and it has three boxes, two of which are empty (or has a goat behind a door, if that helps - I'd rather get an empty box than a goat) and one of which has the keys to a new car. You, as the contestant, have to decide the smartest choice; take a small amount of money and give up your box with its 1 in 3 chance of a new car or risk getting nothing at all. The game show host, Monty, then even reveals one of the three boxes to be empty and offers you a larger amount of money for your still unknown box. Do you take the money, since you seem to have a 50/50 chance of a car or nothing? No, you offer to switch boxes with him. Confounding? Aren't there equal probabilities, since there are only two boxes? Read on...

Yes, I won the car the first try because the math says so - except it shouldn't, if you ask most people. Link: UCSD
Professor Jim Al-Khalili is a Science 2.0 favorite. He has been mentioned here too many times to count because he is the University of Surrey Professor of Public Engagement in Science and the kind of physicist you want to argue with at halftime during Steelers games.
In Paradox: The Nine Greatest Enigmas In Physics, he covers all the good ones, including the difficult Maxwell's Demon along with the more common Grandfather Paradox, were you to go back in time and kill your grandfather, and Schrödinger's Dead And Alive Cat.
It's a breezy 200 pages, an easily digestible book that will still confound you, no matter how clearly he explains it. Along the way, he teaches you how to think a little better.
The Monty Hall Paradox, for example, can be statistically gamed a little - if you have three boxes and Monty Hall knows which one has the car and which two are empty, by opening one to make you feel like better odds, he could be setting you up. If he offers you $1,000 for your box, he may want you to think it has the car and wants to offer you just enough you get greedy and want to hold onto it, assuming it has a much more valuable car, and getting nothing.
By offering to switch boxes you statistically increase your chances of getting the car. Here it is visually using doors and goats.
Of course, this assumes Monty knows which door or box gives you a car. What if even he does not know which box has the car but is instead offering money blindly? You can no longer rely on his prior knowledge and neither can he. What should you do then? You still switch if you can, you'll be right 66% of the time.
Are you a modern netizen and can't fathom these problems in your head? UC San Diego has an online version. Try it as many times as you want but the math rules, just like Roethlisberger in third down passing situations. Or second down passing situations. Basically, if you have three doors in your Monty Hall scenario and all three do not have Big Ben behind them, your chances of Sunday afternoon happiness go way down.
Paradoxes don't make sense? We can argue the specifics all week but if you want to tickle your brain with Fermi and The Twins and the other paradoxes I mentioned here, pick up a copy of "Paradox" and jump into arguments that are sometimes thousands of years old.
 |  |  |  |  |





Comments