You prepared yourself a zillion times. Still it feels like you are placed in an entirely new situation, a nightmare you never considered.
Luke Lucifer the game show host moves closer to you and looks deep in your eyes. His voice is soothing. “I will repeat the question once more. We have two safe deposits. Whatever is left of the 200k in the other safe deposit is yours. But you have no influence on that amount. Your colleague finalist Jude and no-one else will decide whether there will be any money left in there. However, the same applies to you. You, and you alone will decide what will be left in this safe deposit. What is left will be for Jude. You can leave the full 200k in there for him to grab. Or you and me can split the amount: 100k for you and the other 100k goes back to me. Subsequently, we will go to the other safe deposit so that you can take what Jude left there for you. What is your choice? Do you want to add a 100k to the money awaiting you in the other safe deposit?”
Your brain is working at full speed. You can't lose if you take the extra 100k. You just top up the amount waiting for you in the other safe deposit with an extra 100k. No matter what Jude decides, splitting the amount in front of you with Luke will give you an extra 100k. But the same applies to Jude. And if you both take the extra 100k, you both walk away with just that. Half of what you would have had, had you both stayed loyal to each other and cooperated. So it is in your common interest to cooperate and not grab any money intended for the other. But you don't know Jude. You just met him at the show. Can you trust him?
“You can't loose by grabbing an extra 100k” you hear Luke whispering in your ear.
“No!” you yell. Your voice has a strange high pitch to it. “No, I won't take this money!”
Luke smiles. “Let's see then what is your prize remaining in the other room.” He opens the door of the room, and you both walk out. At the end of the corridor you spot Jude and Luke's female assistant leaving the other room. Halfway the corridor you meet. You look Jude in the eye. He looks back at you, and smiles with confidence. You smile back. What a relief, you both got 200k!
You quicken your steps as you approach the other room. When the door opens you dash into the room.
The truth hits hard. The safe deposit is wide open. It's empty. Your adrenaline level rises. Your hands form into fists. “I'll break his legs!” you mutter.
The Prisoner's Dilemma Paradox
Welcome to PD, the prisoner's dilemma. The PD game is a prototypical model in game theory, used to demonstrate that in a world of self-serving individuals cooperation and the emergence of win-win outcomes are far from guaranteed. On the contrary, game theory predicts that rational decisions in PD-type of situations invariably lead to outcomes that are bad for all participants.
This game-theoretical result somehow seems paradoxical, or even wrong. How can it be that rational individuals take decisions that can be predicted to led to poor results? How can two individuals decide not to cooperate when it is in their own interest to do so?
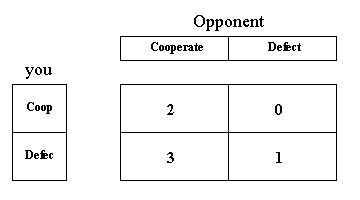
The PD game. Your pay-off depends on your choice to cooperate or not, as well as on the corresponding choice made by your opponent. With no-one cooperating you earn one unit pay-off (bottom right entry). Your decision to cooperate will cost you one unit (compare the top row with the bottom row), whilst the cooperation of your opponent delivers you two units in pay-off (compare the left column with the right column). For the pay-offs used in the game show, each unit in this table represents $ 100k.
People often argue “I would not act in the PD game the way game theory predicts me to act”. However, these people invariably have a game in mind that is different from a true PD. One way or the other they consider potential consequences of their choices that are not part of the PD model. For instance, they implicitly assume that would they defect, their opponent in the PD game will somehow retaliate. Or they consider the game-theoretically prescribed action to contain a hidden cost related to their environment condemning the particular action, or they add a cost related to the fact that they have to keep their actions hidden, or a cost associated to their conscience playing up, etc.
All of this makes the particular games these people consider different from PD. However, when playing a pure PD game there is no escape. No escape from the fact that rational individuals will refrain from cooperation.
However, the non-acceptance of the PD outcome by so many is relevant. In fact, this non-acceptance reveals a weakness in the PD model. More specifically, the aversion against PD points to the fact that this game-theoretical model can hardly be considered applicable to any real-life situations. The above described game show situation should make this clear. Few people act as a patsy, and indeed as we observed in the above PD game show, upon discovering the other player's defection, the 'PD victim' muttered “I'll break his legs!”. Factor in a sure fight resulting from defection with the related costs of hospitalization, and the game changes entirely. Suddenly the choice to take the extra money at the expense of your opponent becomes much less compelling.
From Dilemma to Tetralemma
Let's see how we can modify the PD game to reflect the fact that participants can choose to retaliate. First we review the traditional PD game. Both players have two strategic choices available: cooperate or defect. The pay-off matrix is the 2 x2 table shown above.
The fact that game theory predicts the outcome of the PD game to be both players defect, can easily be checked using a method game theorists refer to as 'iterative elimination of dominated strategies'.* In the game of PD, this iteration consists of one step only: under no circumstance is the strategy to cooperate any better than the strategy to defect. In fact, regardless of the choice your opponent will make, defecting earns you one pay-off unit more than cooperating. So you cross out the row describing your choice to cooperate. As your opponent is in exactly the same situation as you, your opponent will reason the same and also eliminate his choice (the vertical column) for cooperation. The result is for both of you to defect.
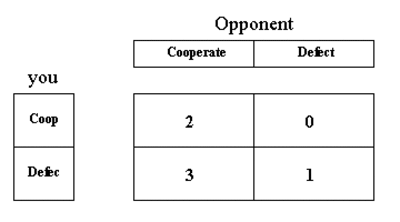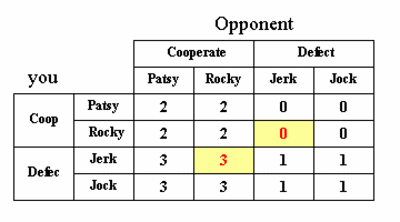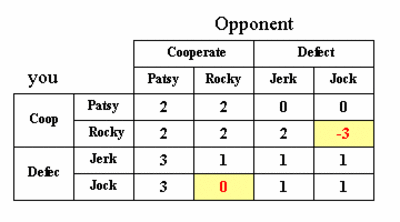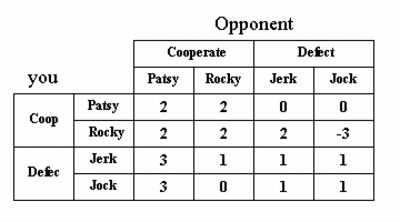
Now, let's add a strategic choice reflecting retaliation to this game. First, we call a spade a spade and re-label the PD choice 'Cooperate' into 'Patsy'. As an alternative to 'Patsy' we add a cooperative strategy referred to as 'Rocky'. The choice 'Rocky' boils down to full cooperation combined with a retaliation action in case the opponent defects. This retaliation consists of demanding the defecting opponent to hand over to you the two units pay-off you would have received would he had cooperated with you. In case the opponent refuses to hand over the two units of pay-off, you will get in a fight that will cost both** three units of pay-off. This will leave him empty handed, and will leave you with a negative pay-off of three units.
In response to this 'Rocky strategy' the defecting opponent has two choices that we shall label 'Jock' and 'Jerk'. Jock represents the choice of not handing back any money, but to get into a fight with Rocky. Jerk represents the choice to hand back the money demanded by Rocky. With the total of four strategic choices, we coin this extended game 'Prisoner's Tetralemma' or PT.
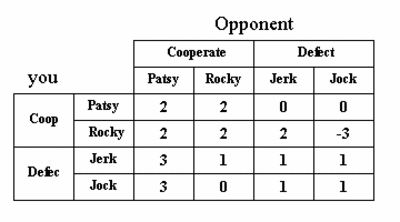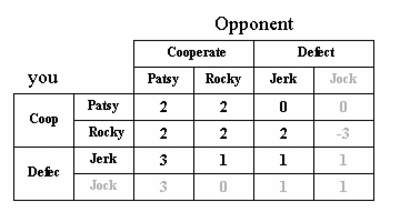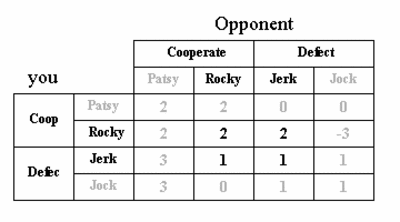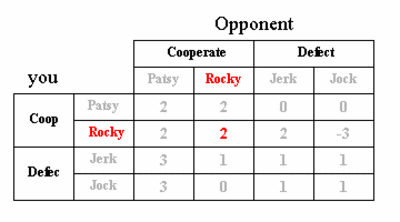
The PT (Prisoner's Tetralemma) game. Iterative deletion of dominated strategies results in the identification of the retaliating Rocky strategy as the rational choice..
At first, it might seem pointless to introduce Rocky as a viable strategy. If one plays many PT games against an unbiased population of the four strategies (25% Patsy's, 25% Rocky's, 25% Jock's, and 25% Jerk's), Rocky comes out as the worst strategy.
Does this mean that we can ignore Rocky as a rational option?
The answer is 'no'. The introduction of the cooperative but retaliating Rocky strategy, whilst not immediately obvious, does perturb the balance between the other strategies such that Rocky does emerge as overall dominant strategy. Iterative deletion of the dominated strategies demonstrates this point. First step in this elimination process is the elimination of the strategy Jock. This strategy is dominated by Jerk (against Rocky, Jock performs worse than Jerk, whilst there is no strategy against which Jock performs better than Jerk). If you come to the logical conclusion that Jock is not a viable strategy, so will your opponent who is facing exactly the same choices. Having eliminated the row and column labeled 'Jock', in the resulting 3 x 3 matrix Patsy is no longer a rational option, as it is dominated by Rocky (check this). So a next round of elimination follows in which Patsy disappears. In the resulting 2 x 2 game, Rocky dominates Jerk, and the latter gets eliminated. The surviving strategy is Rocky. We conclude that game theory predicts that the only rational strategy is for each player to be willing to destroy one's own pay-off (against any opponents following a Jock strategy).
Seek win-win situations, and cooperate freely, but when needed retaliate without considering the cost of doing so. Isn't that exactly us?
What Doesn't Kill Us Makes Us Stronger
It is interesting to speculate how Darwinian evolution has led to lifeforms like ours consisting of strong retaliators. Here we are entering the area of evolutionary game theory. Key result from evolutionary game theory is that for a population to change its behavior towards the fittest (highest pay-off) strategy, does not require that population to consist of rational players. In fact, it is not needed that individuals ever change their behavior or adapt their strategy. All that is required is that individuals reproduce and that those individuals in the population who receive a lower pay-off yield fewer offspring.
Applying these ideas to the above-defined PT game, for a range of starting conditions, the population evolves as shown in below plot. What we see happening here is that the Patsies, who suffer from both the Jocks and the Jerks, have fewest offspring and die out first. At the same time, both the Jocks and the Rockies suffer from their mutual fights, and as a result the Jerks produce most offspring and become the largest group. However, as the Jerks keep growing and provided the Rockies do not die out completely, something interesting happens. At some stage the Jerks and the Rockies combined will outnumber the Jocks by more than a factor four. At that moment, the Rockies start receiving the highest pay-off and will grow fastest in population. From that moment onward there is no stopping the Rockies, and eventually the whole population evolves to 'all Rockies'.
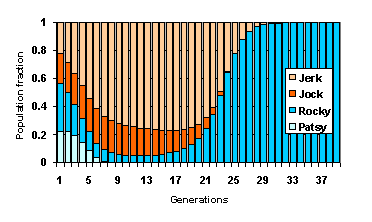
Evolution of the fractional populations in the PT game. Each individual participates in games with all others. None of the individuals ever change their choice of strategy, but those who score badly in the game produce fewer offspring. For various starting conditions, the population involves into 'all Rockies', but in getting there the Rockies have to go through some tough times.
Notes
* An alternative way to derive a prediction for the outcome of the game is to utilize the Nash equilibrium concept (named after Nobel laureate John F. Nash). For the simple games analyzed in this blog post, we don't need this more general approach.** Note that I take care in keeping the game symmetrical: participants that get into a fight suffer the same cost.
------------------------------------------------
More Hammock Physicist articles: The largest distance between two points. What you didn't know about E=mc2. Time's arrow. Quantum telepathy. Booting up the universe. Fibonacci chaos. Powers of six-billion. Quantum virus. The grand arena of physical reality. Game theory and the art of acting rational. Holographic hot horizons. Holographic horizons get hotter. How to get rid of dark energy. Entropic gravity for pedestrians. How to create a black hole. Hubble's 20th.





Comments