Over the course of the past two decades we have witnessed the rise of deep learning as a paradigm-changing technology. Deep learning allows algorithms to dramatically improve their performance on multivariate analysis tasks. Deep neural networks, in particular, are very flexible models capable of effective generalization of available data, with unbeatable results in their predictions. Indeed, from the outside, nowadays it looks as if the game changer in predictive analysis was the construction of large neural network architectures. But it was not.
What really makes a difference in the performance of learning algorithms is what is under the hood, and this might surprise you - it's a tool we have been familiar with for over two centuries. Differential calculus! It is not by chance that among the experts, the term "deep learning" has already been set aside in favor of the more descriptive "differentiable programming".

Differentiable programming consists in endowing your code of a way to trace the effect of change of parameters forward and backward, and ultimately, to navigate those parameters toward values that maximize a utility function. Just specify exactly what you want, and the machine will provide it for you. But be careful - you get what you want, so you have to put all your brain power in specifying _exactly_ what that is. Ultimately, that is where you win: by formulating carefully your utility function!

In a recent article, together with a team of bright colleagues whose average age is a half of my own, we studied with care the problem of measuring the energy of muons in a future collider, where collisions may produce muons so energetic that magnetic bending may not allow a determination of their momentum with useful precision. We could demonstrate that the spatial pattern of radiative losses that muons withstand in a granular, dense calorimeter, contains information which can be exploited. With a deep convolutional neural network we obtained 20% relative uncertainty on the energy of 4-TeV muons, which is enough to retain the value of those particles as sensitive probes of new physics.

During the preliminary studies that led to the above result, we also fiddled with more down-to-earth statistical learning tools to analyze the same data. In so doing we developed an overparametrized k-nearest neighbor algorithm which we endowed with a large amount of flexibility. Indeed, that is the key to provide a good model: it has been shown by Mikael Belkin and others as having a large number of parameters does not really create a risk of overfitting your data - if the number is really large, the minimum of your loss function becomes very smooth, and retains optimal generalization properties. 

In a nutshell, the kNN algorithm is based on the principle of "asking your neighbor". If you want to guess what is the income of a person, take the average of the income of people in your available dataset that share similar characteristics with those of your target: age, home address, feet size - anything may be useful. The idea is that the expectation value of a parameter varies smoothly over the parameter space, so if you can build a local average with data, you have it.

Today, the arXiv features a new paper we produced, where we detail the inner workings of our kNN algorithm on steroids. It is the first time, to my knowledge, that a kNN is endowed with 66 million parameters - to fit just eighteen variables! The algorithm we developed contains a number of innovative solutions, including a non-convex loss function that automatically correct for the nasty estimation bias that is otherwise present in the regression problem we applied it to.

The money plot of this study is shown below. The graph demonstrates that the "simple" nearest neighbor technique can achieve the same level of performance of multi-layer neural networks or gradient-boosted decision trees. As I said above, the power is all in differential calculus - which we used to optimize the kNN parameters.




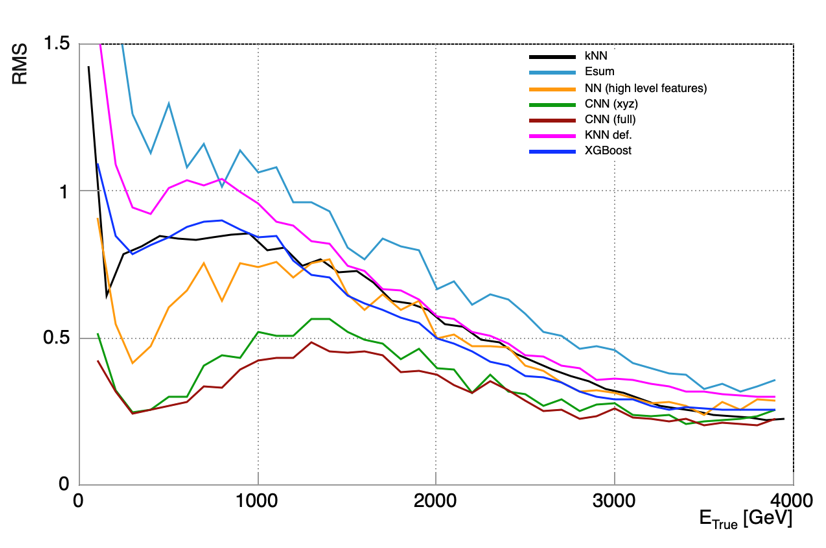
In the graph you can see that the RMS of the muon energy prediction (vertical axis - the smaller, the better) of the kNN we developed (in black) is competitive, especially in the high-energy regime which is the focus of the regression task, with NNs and XGBoost BDTs. The comparison with CNN results (the two curves reaching down to smallest RMS) is only descriptive of the additional power that knowledge of the full granularity of the calorimeter allows - that information was not used for the training of the regular NN, the BDT, and our kNN algorithm.

One consideration remains to be made. While the kNN shows equal performance to NNs and BDTs, of course it is in another league in terms of CPU consumption. The results in the graphs required literally several months of CPU for the kNN, while NN and BDT can train their parameters in just a few hours on the same machine. So why bother? Well, because it is fun, and because it is important to understand that from a mathematical point of view all these tools are one and the same, once you overparametrize them: the real difference is made by differentiable calculus!


---

Tommaso Dorigo (see his personal web page here) is an experimental particle physicist who works for the INFN and the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the MODE Collaboration, a group of physicists and computer scientists from eight institutions in Europe and the US who aim to enable end-to-end optimization of detector design with differentiable programming. Dorigo is an editor of the journals Reviews in Physics and Physics Open. In 2016 Dorigo published the book "Anomaly! Collider Physics and the Quest for New Phenomena at Fermilab", an insider view of the sociology of big particle physics experiments. You can get a copy of the book on Amazon, or contact him to get a free pdf copy if you have limited financial means.