He probably means “space” here, not “space-time”, because space-time already includes time and thus has no further time to do anything, let alone absorb stuff. Let us nevertheless do a sympathetic reading and firstly show what he may mean with a simple example:
Imagine electromagnetic radiation (light) inside a box of volume V = L3. Now remove one of the walls and let the radiation spread out into a larger volume, say V’ = 8V. The energy U of the radiation is conserved: U’ = U. However, if you let the radiation pressure move a plunger instead so that at some point the volume is eight times larger, half the energy goes into the plunger: U’ = U/2.
For those who do not like real formulas, just remember: plunger = taking out half the energy when expanding volume 8 fold.
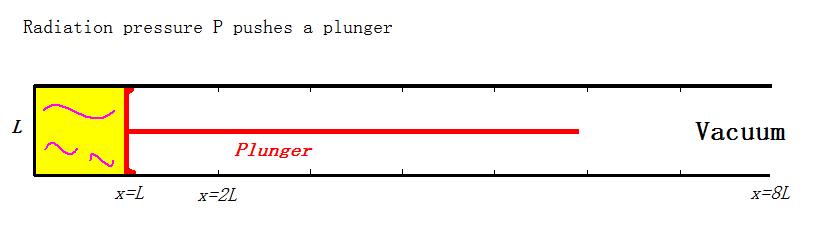
Straw-man: “Why half the energy?”
Sock-puppet: “Consider a column with volume V = L2 x with a plunger of surface L2 starting at x = L with energy U(L). Like in the picture, but note that Sascha was too lazy to draw it three dimensional. Moving the plunger slowly reduces the energy via dU = - F dx = - P L2 dx = - (ρ/3) L2 dx = - [U/(3 L2x)] L2 dx = - [U/(3x)] dx. Thus U = Constant * x-1/3 and hence U = U(L) (L/x)1/3.
At V’ = 8V holds U(8L) = U(L) (1/8)1/3 = U(L)/2.”
Sock-puppet, you scare away my readers! Now let us get to cosmology: Consider a cube of volume V = R3 expanding to a cube twice the length resulting in the volume being yet again eight times more than before: V’ = (2R)3 = 8V. Radiation energy density ρ = U/V is proportional to 1/R4,
where R-3 is for the volume and the further factor R-1 takes care of the redshift, i.e. the stretching of the wavelength of the light. The energy of the radiation is initially U = ρ R3, but after expanding the universe, it is U’ = ρ’ (2R)3. However, because of the redshift, it also holds that ρ’ = ρ/24.
And so we get U’ = ρ (2R)3/24 = U/2, i.e. the expansion takes out half the energy again.
In cosmology, space growing is exactly the plunger, the “space-plunger”.
I will totally rip the argumentation above (and Sean's "solution") apart the next time. Stay tuned.
