Yesterday somebody asked me here if I could explain how does a muon really decide when and how to decay. I tried to answer this question succintly in the thread, and later realized that my answer, although not perfectly correct in the physics, was actually not devoid of some didactic power. So I decided to recycle it and make it the subject of an independent post.

Before I come to the discussion of how, exactly, does a muon choose when and how to decay, however, let me make a few points about this fascinating particle, by comparing its phenomenology to that of the electron.

Muons versus Electrons

The muon is the electron's heavier brother. It has the same charge and the same status of elementary lepton, but the one thing that makes it different from the electron (well, the other is "muon-ness", which does not count for the sake of this argument) changes most of its phenomenology. Such is the importance of mass!

The electron mass is 0.511 MeV, the muon mass is 105 MeV: a factor of 200 in favor of the latter. Let me make a list below of the difference this makes.

1 - The electron does not have anything lighter to decay into: being the lightest electrically charged fermion, it is condemned to live forever. The muon, instead, can turn into an electron (indeed I discuss the process in more detail below). The available energy of the reaction is the factor which dictates its lifetime: 2.2 microseconds. So the electron is eternal, while the muon is unstable. The universe would be an entirely different place if muons were as stable as electrons!

2 - When in possess of energy in the range from a MeV to a few GeV, the electron is already quite relativistic (it travels at the speed of light: 297,000 kilometers, or only inches less than that, per second), while at the same energy the muon is much less relativistic. This fact has several important phenomenological consequences, but discussing them would bring me too far today.

3 - The electron radiates bremsstrahlung photons much more readily than muons at the same energy. Take a W boson produced in a LHC collision: if the W decays to an electron-neutrino pair, the energetic electron will have a penchant to radiate out photons whenever it crosses the electromagnetic field of the atoms it traverses.

The muon, with its 200 times higher mass, is subjected to a 1.6 billion times smaller energy loss by radiation at the same energy. This has important consequences for the detection of electrons and muons: the most visible one is that electrons interact in dense matter by producing a shower of secondaries, as I discussed just a few days ago here; muons, on the contrary, pass almost unhindered through large amounts of material. All particle detectors in collider physics experiments are built the way they are because of this simple difference: dense layers of material are used to detect electrons, while muons may be picked up downstream, where no other particles make it.


So how does a muon decay ?

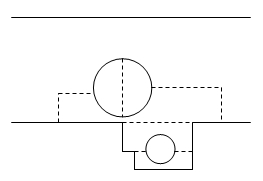We usually picture an elementary particle as a line in a Feynman graph, and we think of it as a point-like object propagating in space along a straight line. But quantum mechanics tells us otherwise: the particle should rather be pictured as a cloud with undefined boundaries. A lot is going on in its neighborhood: not only does the particle interact with the medium, constantly "talking" with the environment by emitting and absorbing bosons, the quanta of the interacting fields: the particle also emits and reabsorbs "its own stuff", virtual particles it generates by itself. The picture on the right should explain what I mean: the upper straight line is what we may think of the muon propagation; the lower graph shows a more realistic scheme, with the muon continually emitting virtual bosons (dashed lines) which occasionally turn into pairs of fermions, etcetera, ad infinitum.

In particular, the muon emits and reabsorbs virtual W bosons of electric charge equal to its own. By doing that, it momentarily turns into a muon neutrino: electric charge and weak hypercharge get subtracted from it, to be given back as soon as the virtual W comes back from the free trip.

Maybe I should explain what I mean by "virtual" at this junction. A virtual particle is not a ghost, or a mathematical trick! A virtual particle, in truth, is as real as a real one; the only difference is that its presence may be ignored when one describes a particle reaction in the simplest approximation.

Now consider that W boson: however virtual, it is also authorized to temporarily split into fermion-antifermion pairs before it is claimed back by the emitting muonic line. It may thus turn into an electron- electron neutrino pair, for instance; but also other fermion pairs are possible. Then, before you know it, the pair fuses back into the W, and the W fuses back with the muon neutrino to yield the original muon. This is shown graphically on the right.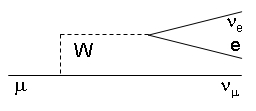

But with electron-neutrino pairs one different thing may happen: the duo may decide to leave the scene of the virtual fluctuation for good, never fusing back into the W. They do so without violating indefinitely the energy-momentum conservation law, because the total mass of the muon neutrino, the electron, and the electron neutrino is smaller than the original muon mass. So the muon gets fooled: the quantum numbers it lent to the W boson are lost forever. It is effectively turned into a muon neutrino for good.

Muons, as any other subatomic body, constantly emit and reabsorb virtual particles of all the kinds they couple to. The probability that a virtual W plays the disappearance trick to the muon which popped it out of the vacuum is constant every time it gets created: this creates an exponential decay law, no less than the one which applies to the stack of tokens that a unwitty player continues to bet on "red" at the roulette as he wins.

What governs the speed of the disappearance, i.e. the muon lifetime, is a direct consequence of the likelihood of the transition discussed above, which in turn depends on the available energy of the reaction (muon mass minus mass of the final state bodies), as well as the strength of the coupling: the latter is a direct measure of the likelihood of virtual W emission.

Taking Stock

All in all, there is nothing particularly surprising in the description I have provided above: particle reactions readily occur if they do not violate any quantum-mechanical rule. Muons may only decay to electrons -the only particles lighter than muons which carry the same electric charge- and they do so by means of the exchange of a W boson, the carrier of the electroweak charged-current interaction.

Once you understand how muons decay, it becomes absolutely trivial for you to figure out that a b-quark may decay to a charm quark, an electron, and a neutrino: the diagram and the qualitative explanation are the same. But the large mass of the b-quark (4 GeV, 1.2 of which get converted into the mass of the charm quark) also allows different leptons to be produced: a muon-neutrino pair, for instance. A tau-neutrino pair is also possible, but its rate is sizably smaller, since the tau lepton weighs 1.77 GeV, which means it takes away a rather large share of the available energy.

In conclusion, the decay of elementary particles may be understood without the complicated calculations of quantum field theory. A qualitative picture may explain most of the observable features of the process. However, it is quantitative calculations what actually tell us, once compared with experimental measurements, that our qualitative picture is correct!