Those of us who work on quantum gravity focus on the one observable phenomena where everyone expects quantum effects and relativistic effects to be of equal significance, black holes. Bekenstein and Hawking did this back in the 1970's and defined what is known as black hole thermodynamics. In a nutshell once Hawking had shown that black holes radiate they both found that they obey the laws of thermodynamics.
All the stories about firewalls, information loss, etc go back to that insight. So far any observations we have been able to make confirm their hypothesis making it a reasonably strong theoretical touchstone. Being able to reproduce the results of black hole thermodynamics is only the first tier plausibility argument that any hypothesis advanced regarding unification of Quantum Field Theory and General Relativity must pass.
Relativization black holes a bit cooler than we thought.
In my latest work open for comment and still changeable on "The Winnower" Fundamentals of Relativization II with Computational Analyses I have used Wolfram's Mathematica to carry out a careful computational analysis of the black hole problem using my model. The goal was to test whether using my postulates and making basic assumptions would be enough to reproduce black hole thermodynamics. In particular would I be able to get the same temperature curve as Bekenstein and Hawking.
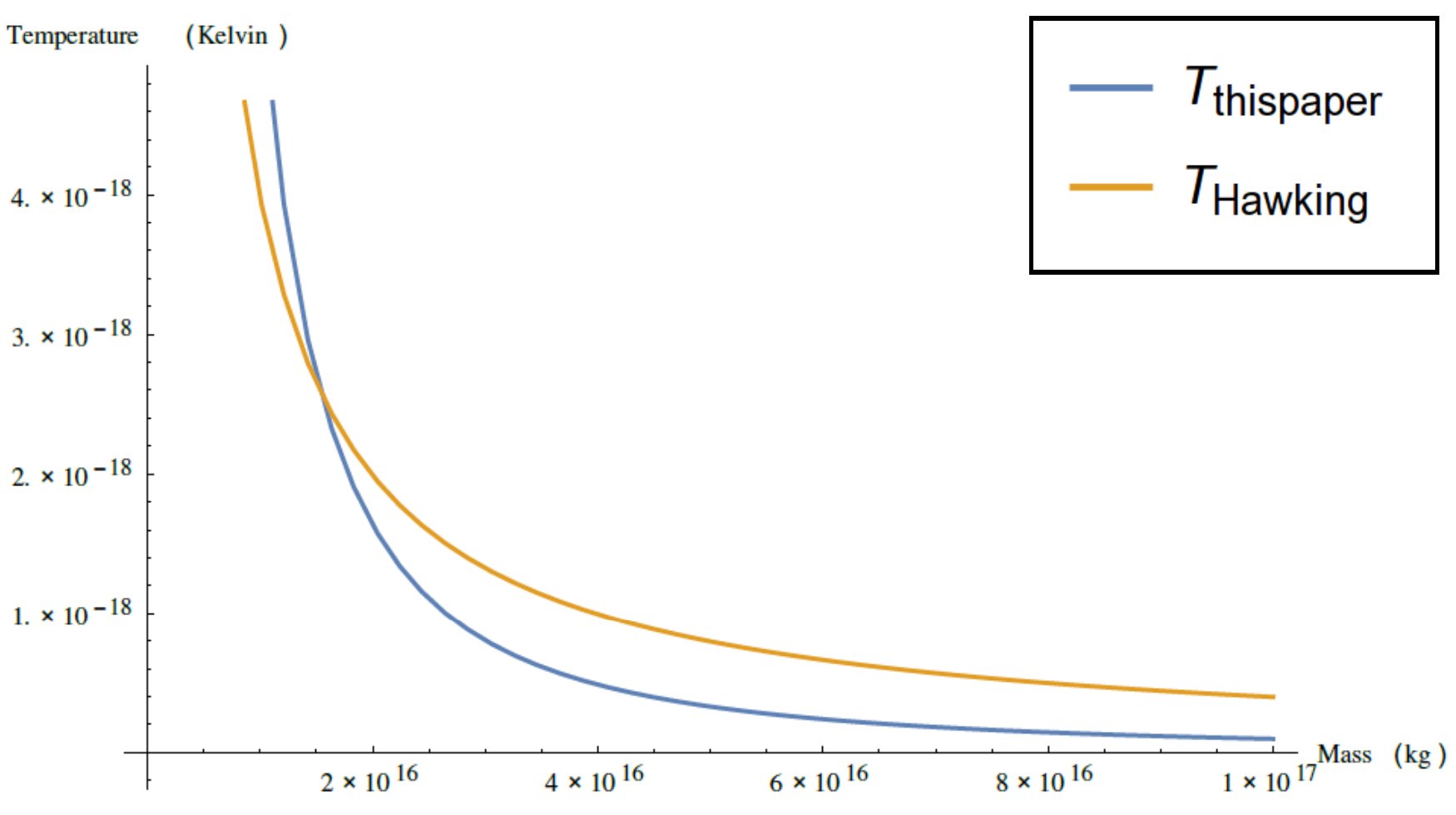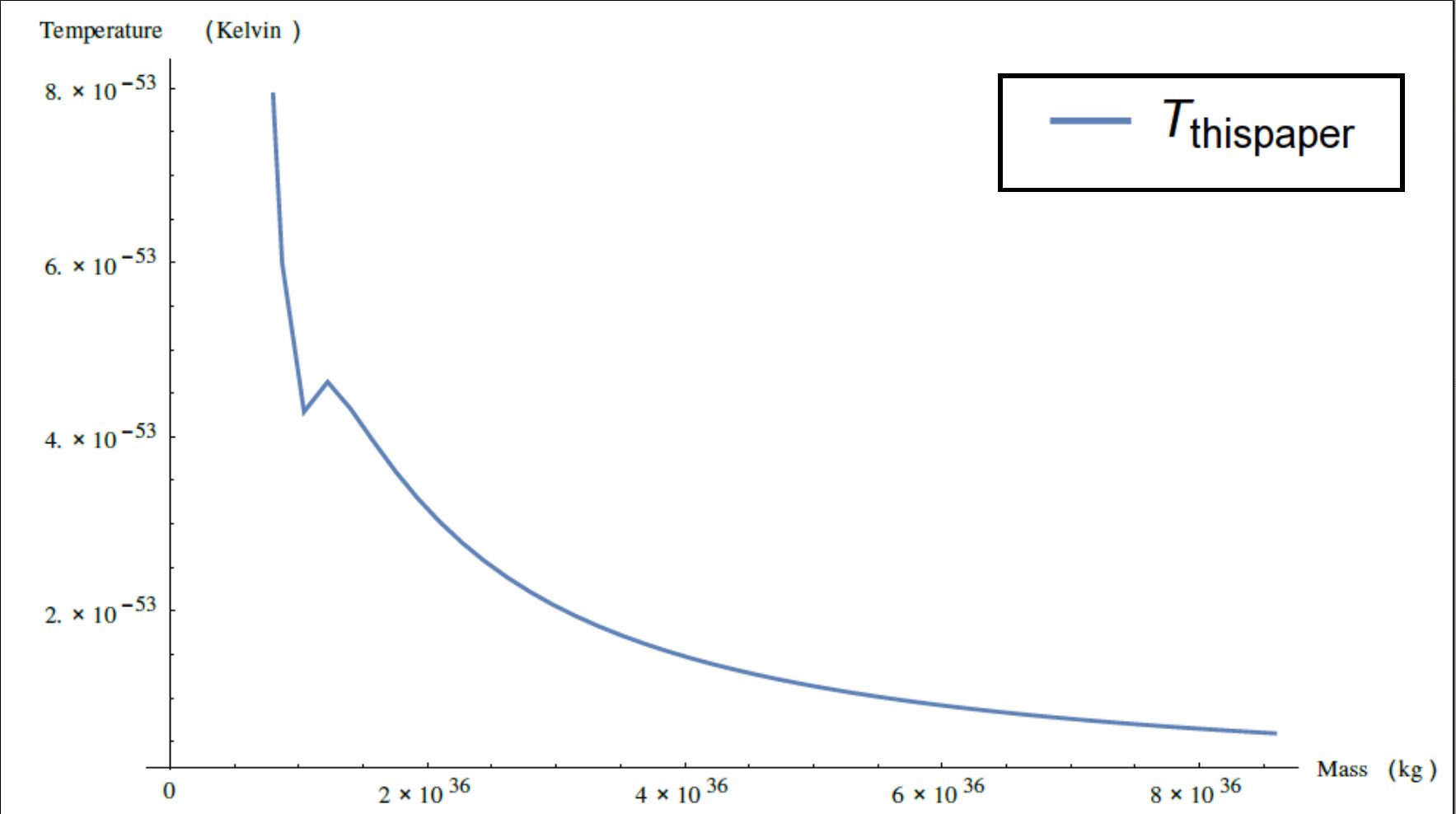
This is very very close to the accepted semiclassical calculation. Notice however a lower masses my model predicts that they should be much hotter. The following figure shows a larger range and only the model derived from the postulates of relativization. Notice there is a little zig-zag in the model. In addition to predicting a slightly lower temperature for black holes this one predicts that going from about 10% of the mass of Sagittarius A* to 13% or so there will be a slight upward jog before once again proceeding downwards.
Regarding the objections of the reviewers to the very concepts of the Fundamentals of Relativization.
First of all, I must insist that anything resembling a "review" on this article be posted at "The Winnower". Part of the whole academic rigor of that process is the reviews and comments and replies to comments. So let it be know I will remove anything like a review from here. Questions and comments directly on the content of this blog post itself are very welcome.
Prior to submitting the first article in this series to The Winnower I did submit to a well known scholarly open access journal. One which is associated with a well known institution/society of people who study physics. It does not matter which one. Rather mysteriously two editors said this work was “incremental”, the third felt it did not make sense. (A sign of genuine review is that at least 1/3 of experts won’t agree on a paper one way or the other.) I did not ask incremental building on what. At that point the opportunity to publish on The Winnower arose.
After a careful reading of a very fine textbook on String/M-Theory the very concepts of relativization are not totally new or unique. What is new is my insistence that then Einstein Equivalence principle would be promoted to a basic principle of nature in such a formulation. Which I implemented by switching the roles of Poincare-Lorentz invariance and Diffeomorphism invariance. In standard String/M-Theory Poincare symmetry is the global symmetry. In this model there is global diffeomorphism symmetry and local Lorentz symmetry. I have not used the language of branes and strings and world sheets etc up to this point. Just spaces and manifolds of different kinds coexisting at the same time in the same equations. This has confused people that is my fault.
It may be that not being constrained by the standard language and visualizations has allowed me to make progress, but hinders communications.
However, as the plots above show this model passes the basic computational test of black hole thermodynamics. It extends it by predicting the same effect as the semiclassical Bekenstein-Hawking formulation and predicts an effect for very large black holes that may one day be observable.
TL;DR: My own calculation of black hole temperature as a function of mass shows that they will be cooler than predicted by the accepted theory. My model also predicts that very low mass black holes, ones which could possibly be created directly in a lab will show a higher temperature than predicted from the Beckenstein-Hawking formula T=1/(8 pi M). However my calculation shows the same general trend and is in overall agreement with the accepted model. So much for my model being "nonsense". Nonsense does not predict nature.
Footnotes:
- String theory and m-theory a modern introduction. Cambridge University press.External Links: Document, Link Cited by: Introduction.
Comments