There is an important difference related to the mathematical formulation of Self-Field Theory (SFT) and that is the complete absence of gauge. We know from the various quantum theories that gauge plays a crucial role. To understand this difference we must first look at the basics of gauge theory. And to look at the basics of gauge theory we must first define some terms we have already used in discussing SFT. First let’s define Maxwell’s equations.

_                    (1a)                                                                             

                      (1b)

    (1c)

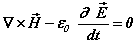    (1d)

If we just look at the equations above (1a-d), Maxwell’s equations (the inhomogeneous Maxwell's equations), then we have a basis for examining gauge in various systems. The reason being, as they stand, these equations cannot be solved uniquely. Since all equations involve differentials (without the actual variable) there is no definitive form of the equations. In other words, there is a family of solutions, all isomorphs of each other; we do not have a unique solution. We can add any constant we like to them and this will be part of the overall family. Now this is the basis of gauge theory with its symmetries. In terms of SFT, two arbitrary spinors could be a solution as long as they obey the Maxwell equations in (1a-d) above; the solutions 'float' about constants of integration. There is a freedom to choose the constants anyway we like.

So what is a Maxwellian? 

In addition to the inhomogeneous Maxwell equations where 

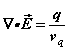becomes (1a) and 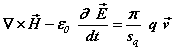becomes (1d)

we use the Lorentz equation that describes the field forces acting on the particles is written as

(1e)

where the constitutive equations in free space are
                      (1f)

.                      (1g)

the relationship between the speed of light [i] and the ratio of the fields

                      (1h)

and finally the atomic energy density per volume is

(1i)

which depends upon the E- and H-fields in the atomic region. Equations (1a–i) are termed the Maxwellian, or sometimes the EM field equations.[ii] In these equations, v is the particle velocity, m is its mass. It is assumed that the volume of integration v_n over which the charge density is evaluated, and the area the charge circulates normal to its motion S_n, are calculated during successive periods over which the internal motions of the atom take place. 

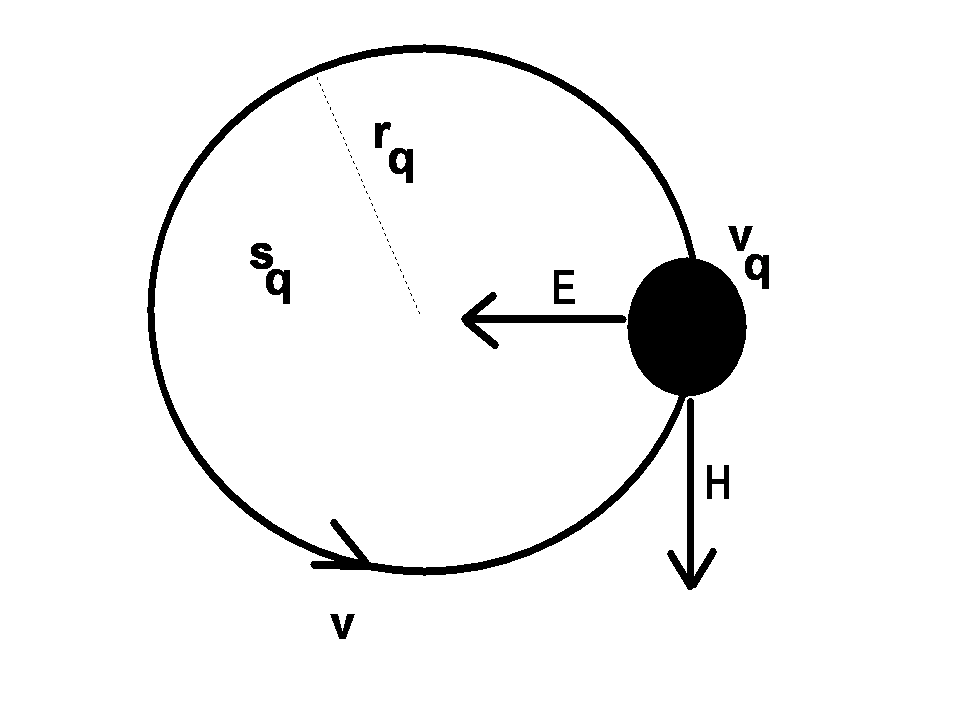
In the Maxwellian, (1a-i), where we use the inhomogeneous forms for (1a) and (1d) there is no gauge because now the the fields are completely defined. We have a unique system of equations. There is no family of isomorphs because we have tied the bispinorial solution down; it is no longer a floating family of similar shaped solutions, but a single unique solution. 

This is a crucial difference between quantum theory and SFT, a complete absence of gauge, basically due to the use of the Lorentz equation within SFT along with the other defining equations (1e-i). That said, gauge theory has been a very important tool when searching for links between the forces found within nature, for instance when it is used within the Standard Model of particle physics. The Maxwellian has an analog within quantum theory and that is the Lagrangian.

 [i] In SFT, the speed of light is not proscribed from being variable.  Depending on the energy density of the region being studied, and the photon state, c can vary.  

[ii] Where a nebular current density is used in (2.1d), the factor 4p comes about from an application of Green’s theorem leading to a surface over the volume enclosed by the charge density.  For the case of discrete charges, the factor p represents the area enclosed by the moving charge point.