
One of the things I have struggled to learn is about the real numbers and the group Z2 which consists of only two numbers, {-1, +1}. It still sounds like an empty statement to discuss the group Z2 over the real numbers. The group Z2 is a way of introducing the minus sign to a set that only has positive values, yet the real numbers already have a sign, so nothing is accomplished by the group. Math is a game of intellectual minimalism, so the mention of the group Z2 can be deleted, and nothing is altered about one's understanding of the real numbers.
I began to think about the positive real numbers with the group Z2 serving as a basis.
Here is my notation for this situation, with the u, v, and w in bold italics serving the roles of my combination of the positive real numbers and Z2:
v = a{-1} + b{+1}
u = c{-1} + d{+1}
w = e{-1} + f{+1}
a-f >= 0
Why didn't I just call these vectors? The definition of a vector space says that would be illegal. The positive real numbers are not a mathematical field, and a mathematical field is required for a vector space. Ergo, I am not working with a vector space. Let's see if these structures are "nice" despite that flaw. I will call them proto-vectors because they are not vectors over a mathematical field, but they sure have lots of the properties of vectors. Let us go through the list of properties found on the wiki page for vector space.
They can be added together, and multiplied by a positive scalar:
v + u = (a+c){-1} + (b+d){+1}
v + w = (a+e){-1} + (b+f){+1}
u + w = (c+e){-1} + (d+f){+1}
s v = s a{-1} + s b{+1}
1. Associativity of addition:
u + (v + w) = (u + v) + w = (a+c+e){-1} + (b+d+f){+1}
2. Commutativity of addition:
u + v = v + u = (a+c){-1} + (b+d){+1}
3. Identity element of addition:
0 = 0{-1} + 0 {+1}
v + 0 = a{-1} + b{+1}
4. Inverse elements of addition - here is where I tripped up before.
[method sidebar]
My first reply to this issue in a comment was right, but since I have very little self-confidence, when challenged I will often go down other roads to see where they lead. If it is a dead end, I go back to the start point. Drives some readers nuts, but it is a way to explore. It is also a way to decimate one's reputation. My reputation is of no economic value to me, so I'd rather feel like an issue was examined completely than just take the one direct path to a truth others follow by rote.
[end sidebar]
Here at least is the wiki definition of this property:
For every v in V, there exists an element -v in V called the additive inverse of v, such that v + (-v) = 0.Note, those were statements all about vectors.
What I am going to do now is quote from "The Skeleton Key of Mathematics" by D. E. Littlewood, a book recommended by Barry Barrett. Littlewood is discussing the transition from the positive integers to the signed integers.
The integers so far have no signs, and the impossibility of subtracting say 3 from 2 is sometimes inconvenient. This inconvenience is felt especially by a man with £2 in a purse who needs very urgently £3. He could evade the difficulty perhaps by keeping his money in a banking account. Then having a balance of £2 he could write a cheque for £3 and leave a negative balance of £1.
Consider how this is possible in a banking account but not with money in a purse. The bank associates two totals with each customer's account, the total of moneys credited and the total of moneys withdrawn. The net balance is then regarded as the same if, for example, the credit amounts to £102 and the debit is £100, as if the credit were £52 and the debit £50. If the debit exceeds the credit the balance is negative.
This model is adopted in the definition of the signed integers. Consider pairs of cardinal numbers (a, b) in which the first number corresponds to the debit, and the second to a credit.
A definition of equality is adopted such that
(a, b) = (c, d)
if and only if a+d=b+c.
Addition is defined by the rule:
(a, b) + (c, d) = (a + c, b + d)
and multiplication by (a, b) * (c, d) = (a d + b c, a c + b d)
then the pair (0, a) or any equivalent pair is denoted by a, and the pair (a, 0) or any equivalent pair by -a.
Alternatively, the signed integers could be regarded as a transition from one cardinal integer to another, e.g. the transition 100->102, or 50->52 is denoted by +2, and the transition 102->100 by -2. The definition as a pair of cardinal integers is well adapted to this interpretation.
The positive real numbers and the reals are a generalization of this quote. What is interesting is seeing what these look like in the proto-vector space.
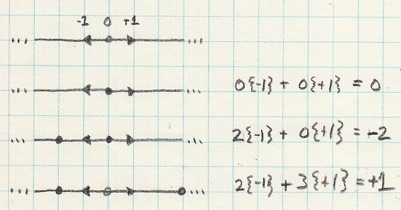
The real numbers are somewhat like line segments in this representation. The start is defined with the {-1} proto-vector, and the end by the {+1} proto-vector. These are not exactly like line segments since the notion of distance is different.
We are in the position to ask if every proto-vector has an inverse.
This raises a question whether 3{-1}+3{+1} is equal to the zero vector. The question can be answered by using equality as Littlewood defined it:
[Note on notation and meaning... I will use three equal signs, ===, to indicate that these are equal when one is also employing equivalence classes. An equivalence class reduces the dimensions of the space.]
[Additional note: the === should only be used when going from the 2D proto-vector space to the 1D real number field.]
3{-1}+3{+1} === 00{-1}+0{+1} === 0
if and only if:
3 + 0 = 3 + 0
Looks good.
5. Distributivity of scalar multiplication with respect to vector addition
s(u + v) = su + sv = s((a+c){-1} + (b+d){+1}) = s(a+c){-1} + s(b+d){+1}
6. Distributivity of scalar multiplication with respect to field addition
(s + t)v = sv + tv = (s + t)a{-1} + (s+t) b {+1}= s a{-1} + s b {+1}+ t a{-1} + t b {+1}
7. Compatibility of scalar multiplication with field multiplication
s(t v) = (st)v = s(t a{-1} + t b {+1}) = s t(a{-1} + b {+1})
8. Identity element of scalar multiplication
1 v = v = 1 (a{-1} + t b {+1}) = a{-1} + t b {+1}
The proto-vectors - proto because the positive reals are not a mathematical field - are quite well behaved. But they also have the properties of the group Z2. Write out its multiplication table:
| x | 1 | -1 |
| 1 | 1 | -1 |
| -1 | -1 | 1 |
Now we can officially and completely legally multiply two proto-vectors together. The results are identical to what Littlefield suggested, even if written in a different notation:
v x w = (a d + b c) {-1} + (a c + b d) {+1}
There is a multiplication identity for the group Z2, good old +1, or 0{-1} + 1{+1}:
v x 1 = (a 1 + b 0) {-1} + (a 0 + b 1) {+1} = a{-1} + b{+1}
Does every element has a multiplicative inverse? Do two simple cases first, ones where the number is like -2 or +3:
Negative example:
v = a{-1} + 0 {+1}
v-1 = 1/a {-1} + 0{+1}
v x v-1 = (a*0 + 0*1/a){-1} + (a*1/a + 0*0){+1} = 0 {-1} + 1{+1} = +1
Positive example:
u = 0{-1} + b{+1}
u-1 = 0{-1} + 1/b{+1}
u x u-1 = (0*1/b + b*0){-1} + (0 * 0 + b * 1/b){+1}
Two down, just one more case to go: what if neither of the coefficients in the proto-vector is zero? There's a fun puzzle. Give it a try.
OK, few will be willing to do so, but a little thought brings up the follow riddle: the term from the product of a non-zero proto-vector and its inverse hat goes with {-1} doesn't want to be zero. This is where we need to Littlewood's definition of equality:
[True if one uses equivalence classes]
0{-1} + 1{+1} === +1
e{-1} + (e + 1){+1} === +1
if and only if
0 + (e + 1) = 1 + e
That will always be true [with equivalence classes]. Now look at the product of a proto-vector and its inverse:
v = a{-1} + b{+1}
v-1 = c{-1} + d{+1}
v x v-1 = (a d + b c){-1} + (a c + b d){+1}
An inverse can be found if the following equations hold:
(a d + b c) = e
(a c + b d) = e + 1
[From CuriousReader below:A quick road to the inverse is to subtract one from the other, then:
(a d + b c) - (a c + b d) = 1
(c-d)(b-a) = 1
(c-d) = 1/(b-a)
Nice, quick and direct.]
I did get a little lazy and ask Mathematica to solve the two equations for c and d:
c = (a + e(a - b))/(a2 - b2)
d = (-b + e(a - b))/(a2 - b2)
Will c and d always be positive? It all depends on the value of a, b, and e. Let's assume a is greater than b. In that case, c is always a positive number, a required thing since I am using the positive real numbers. The value of d does depend on picking a legal value for e:
d > 0
if and only if:
e >= b/(a - b)
This idea is so new to me, I wanted to see it work with numbers. Let a=3, b=1, and e = 1. The value for e is OK since 1 > ½.
c = (3 + (3-1))/(3^2 - 1^2) = ⅝
d = (-1 + (3 - 1)) /(3^2 - 1^2) = ⅛
(a d + b c) = e
(a c + b d) = e + 1
(3 * ⅛ + 1 * ⅝) = 1
(3 * ⅝ + 1 * ⅛) = 2
(3{-1} + 1{+1}) x (5/8{-1} + ⅛{+1}) = 1{-1} + 2{+1} === +1
[Note: the check on the last equality is the sum of the outies must equal the sum of the innies, and 2 does equal 2.]
I can well imagine that some of my dear readers will be upset by the freedom to set e at any value that happens to be greater than a half. I find that property interesting because it surprised me. For those who want to always find the same multiplicative inverse, all one has to do is impose the rule that the value for e is exclusively the equality.
c = (3 + (3-1)/2)/(32 - 12) = 1/2
d = (-1 + (3 - 1)/2) /(32 - 12) = 0
(a d + b c) = e
(a c + b d) = e + 1
(3 * 0 + 1 * 1/2) = 1/2
(3 * 1/2 + 1 * 0) = 3/2
(3{-1} + 1{+1}) x (1/2{-1} + 0{+1}) = 1/2{-1} + 3/2{+1} === +1
This calculation is easier, zeroes are our friends.
What happens if e is less than a half, what is that multiplicative inverse? Well, it just cannot be done with the group Z2 over the positive real numbers.
The previous section on inverses was written as I was figuring it out. It later occurred to me that finding the multiplicative inverse should be trivial because it is trivial to do with the real numbers. If you have picked up the pattern, the inverse of this Z2 over the positive reals should take you all of two seconds:
1/(2 {-1} + 5 {+1}) = ?
The answer is at the end.
What do I think has been done in this exercise? I think the group Z2 over the positive real numbers is a 2D way to represent the mathematical field of real numbers. The two basis vectors are linearly independent, so any non-zero value in one cannot be represented by the other (the two do share zero).
In physics, one is always talking about the differences between two values. It is differences in energy we see, not an absolute measure of energy. Space and time are not absolutes, so we deal with differences between the two.
Calculus requires the properties of a mathematical field. The group Z2 over the positive reals is like the step before having a mathematical field. So what is calculus acquiring in this transition? I think of zero as the location of an observer in time or in space. As an observer in time, negative is the past, positive is the future. The past is fixed, the future is not here yet, so only at time zero can there be change. As an observer in space, there may be things on the left. Whatever is on the left is spacelike separated from whatever is on the right. The only chance for things on the left to interact with things on the right is through the observer.
It may not be worth anything, but I am enjoying thinking of the real numbers as a 2D proto-vector space.
Doug
Answer:
1/(2 {-1} + 5 {+1}) = 0 {-1} + ⅓ {+1}





Comments