Leonard: "The holographic principle suggests that what we all experience every day in three dimensions may really just be information on a surface located at the farthest reaches of our cosmos. So it's possible that our lives are really just acting out a painting on the largest canvas in the universe." 
Penny: "Hmmm..."

Is our universe holographic? Is what is happening in the universe somehow encoded on its boundary? Are we 3D renderings of some distant 2D image? Black hole physics certainly suggests so. But how does such an encoding work? Can we visualize a system that "just acts out" a painting on its boundary?




Have a look at below picture. You see a tiling of 40 squares. Each square is colored yellow or green. How many such tilings are possible? Well, that's easy. With 40 squares to color, and two choices of color, a total of 2^40 = 1,099,511,627,776 colorings can be generated. 


This assumes no constraints apply and the colors can be chosen randomly. Inspecting the figure more closely, however, reveals a constraint does apply and therefore the count is way off. The correct answer is that no more than 2^16 = 65,536 colorings are allowed. Or more specifically: once you fix the colors of the 16 squares at the boundary, the colors inside are also fixed. The interior is "just acting out" what is painted on the boundary.

What is going on here?

Let's take a closer look. The colorings don't really look random, do they? Squares of the same color tend to cluster together locally. If you carefully investigate the picture, you might find a 'local color rule' applies. Can you spot this rule? Right. Every cross-shaped cluster of five squares (consisting of a central square and its four nearest neighbors) contains an even number of green cells. Check this. Each cross of five squares centered around one of the 24 interior squares contains 0, 2 or 4 green squares. There is no exception. It seems we have stumbled upon a 'hard rule'.
This local rule 'propagates' color information from the boundaries into the central region, and thereby fixes the colorings of all 40 squares. The net result is that each allowed coloring of the whole pattern is in 1:1 correspondence with the colorings of the 16 boundary squares. For instance, if we select all boundary colors to be yellow with the exception of one specific boundary square colored green, a single unique color pattern emerges. Two examples of such 'single green boundary square' patterns are shown below.


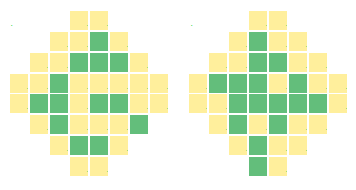
We can mirror image and rotate the two patterns shown above, leading to a total of 16 unique colorings that contain exactly one green boundary cell. These 16 patterns can be used as building blocks for the construction of all 2^16 allowed patterns. 

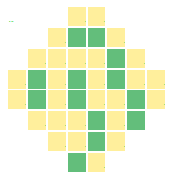
Key observation here is that allowed color patterns can be superposed (added together) into new patterns that are again allowed. This adding of colors is defined as: yellow + yellow = yellow, green + green = yellow, and green + yellow = green. This works thanks to the fact that with this definition of color addition, the 'local color rule' can be written "the sum of colors of a square and its four neighbor colors equals yellow". Below figure shows the result of the addition of the above two 'single green boundary square' patterns. As expected, the resulting pattern does satisfy the prescribed local coloring rule, and contains two green boundary squares.


With 16 distinct 'single red boundary square patterns', each of which can be included or excluded into superpositions to be formed, a total of 2^16 patterns emerges.

Thus we have created a holographic toy model. A universe of colored squares in which each coloring of the 1-dimensional boundary gets mapped onto a single coloring of the 2-dimensional interior region. The laws for coloring the interior are qualitatively different from the coloring description at the boundary. The boundary color law boils down to the simple description: "generate a random pattern of red and green squares". The interior coloring description reads: "cluster together squares of the same color such that each cell combined with its four neighbors contains an even number of green cells". 

Now we can push this idea a bit further, and add a time dimension perpendicular to this holographic sheet. So on top of a holographic sheet of yellow and green cubes (satisfying the even number of greens rule), we build additional layers of yellow and green cubes according to a binary cellular automaton rule. The precise rule chosen doesn't really matter. What results is a universe of yellow and green cubes that follows the equivalent of Bousso's 'causal diamond holographic principle'. Effectively what we have obtained is a toy model for 2+1 dimensional spacetime emerging from a holographic sheet. A universe emerging from a holographic Big Bang. 

The Hammock Physicist on Twitter: @HammockPhysics