The following parallelepiped was found by Clifford Reiter und Jorge Sawyer (Lafayette College, Easton, Pensilvania) with brute force computer trials.

It is a parallelepiped with all three sides being natural numbers. How the hell can it also have all surface diagonals AND all internal diagonals being relatively small natural numbers? Notice that there are two diagonals per surface! Just deforming until one diagonal is natural will not do the trick, not even for just a single surface. There are three of those AND four internal diagonals. How can this ever work out at all? Is this some infinite (in the sense explained below) coincidence in mathematics?

When writing on fine tuning and proper coincidences, I could have been more careful, and divide into three or more types of “cosmic coincidences”, i.e. those mysterious cases in fundamental physics where an important parameter P equals another, seemingly unrelated parameter Q, although P could be much different from Q as far as we know:

Type 1) “Creationist Coincidence”: Q is the golden ratio between log(7pi) and the number N of words in the bible. Scientists avoid the bible, but logarithms, factors of 2pi, and taking square roots come in handy.

Type 2) “Uninteresting Coincidence”: Q changes from a value that is for instance smaller than P to ever larger values. It just happens to be equal P today – well it had to be at some point. There are about a gazillion parameters, so there got to be some such coincidences at any point in time. No reason to get your pants in a knot about them.

Let us get to the more interesting ones:

Type 3) “Fine tuning/anthropic”: Q is a value that is necessary for observers to have evolved at all. Also not so interesting.

Type 4) “Interesting Coincidence”: Q might be intimately connected to P by something underlying that we do not know yet, but this could be wishful thinking after all.

Fine tuning can always potentially be explained away by anthropic arguments. Sometimes, like in the case of the flatness of the universe, this turns out to be an ad hoc “just so” story that is too lazy to find the real reason, which in the case of flatness is cosmic inflation.

So finally, we are left with type 4), the interesting coincidence. Of course, many an interesting coincidence turns out to be something trivial or even something we in a sense did know, had all the laws of nature already figured out for, but still were not making the proper connections for. But there are some interesting coincidences, like with the Hubble constant H discussed the last time, that hint at new, fundamentally important insights.

Most scientists believe that underlying symmetries are always responsible for what seems coincidental in fundamental physics and mathematics. Is this religious? Well, let me hear your opinions on it! But first consider that coincidence in mathematics can imply something infinitely
unlikely. There are infinitely more irrational numbers, like Pi, than rational numbers, like 1/7. And in turn there are infinitely more rational numbers than natural (or integer) ones like n = 5 in any small stretch of the continuous line of numbers, say that from 1 to 10, just to present an example. How often will cutting the range randomly somewhere will get you a natural number like 5 rather than the cut going through at an irrational number like 4.594726518….. ? Never; the probability is zero!

Lets see how that works: Go 3 units along the x-axis. Now climb up the y-direction in unit steps. First you get to (x,y) = (3,1). There is a triangle now.

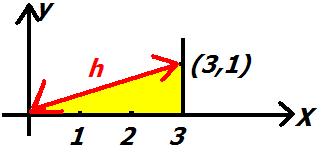
One side is 3 units and the other side is 1 unit. How long is the third side, the hypotenuse h, i.e. the distance from the point where you climbed to at (3,1) to the origin at (0,0)?

Straw-man: “Let me measure it, 3.16… whatever, the length is an irrational number anyways, because you basically picked it randomly: a drunken walk three steps to the right, a stumble ahead to regain your balance. There is zero probability to pick one out of a few natural numbers just randomly from an infinite heap of distances. And if you stumble further to (3,2), the hypotenuse h is not a natural number, and at (3,3) it is also not. Is that what you want to get at?"

Sock-puppet: “But at the fourth trial already, at (3,4), h is 5 units long! A super coincidence! It should not have happened; the probability was zero.”

We do not believe in coincidences; we know there is a reason, some symmetry. Pythagoras’ theorem holds that the square of the length of the hypotenuse h² is the sum of the squares of the other two sides, 3² + y². Therefore, h² is always a natural number if y is natural. No wonder that soon we may hit an h² that moreover happens to be a square. Indeed, 3² + 4² = 5².

Whenever we know the reason, we feel that there is no coincidence, but a good explanation. Whenever we do not know the reason, we believe there must be a reason somewhere. However, looking again at the parallelepiped at the beginning of this article, one may be excused for doubting that there can be a reason similar to Pythagoras. Indeed, the explanation in that case is not known. Of course I bet that there are good reasons, but why am I so sure?

That I maybe should not be I will discuss the next time in this trilogy on “cosmic coincidences”.

More from Alpha Meme on ADHD Yoghurt, Upside Down Planes, ADHD&Drug War, Xmas Sh*t, Vaccines & Bill Maher, Drugs as Citizen Science, Existence, Smolin vs. Susskind, Natural food, Plagiarism, Dark energy, GM food, Microwave Ovens, Asia’s Science, Singularities, Lottery Wonders, Energy, Sex, Quentin Tarantino, Event Horizon, Impact Factors, Chinese, Cheating in Science, Duality and Dimensions, A. Pickering, Black Holes, Energy Non-conservation, More Cheating, 9/11, H. Putnam, Brains in Vats, Metric Expansion & Energy, Coincidences, Error Analysis for Cheating, Hallucinogens, New Dark Age, Inflation << c, Inflation, Fine Tuning, The Boring Universe