Have a look at below picture. You see a binary pattern. This pattern is formed by a hexagonal pattern of empty (yellow) spots and blue disks. The pattern repeats. If you carefully inspection the figure, you will discover that the repeating unit consists of 31 spots (with 15 of these empty, and 16 occupied). Let's consider a simple question: How many bits do you need to fully specify the image displayed?
Regular readers of this column know where I am heading. Yes, we are going to determine the entropy of the pattern. Even if you only occasionally visit this blog, you should know what entropy is. To jog your memory: the entropy of a system is the minimum number of bits needed to describe it. So tell me: what is this entropy for the pattern shown?
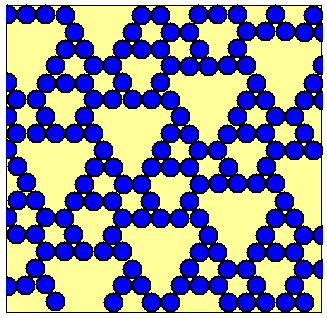
How many bits do you need to specify this binary pattern?
Do I hear 31? That seems a reasonable and logical answer. Although the pattern is stretching indefinitely in both planar directions, we only need to specify the presence or absence of disks for the repeating pattern. This can be accomplished with 31 bits. So, there we have the bit count or the entropy.
You better try again.
The number 31 is way off. The answer would have been 31 in case the presence or absence of disks would result from repeat coin tosses. But coin tosses are unlikely responsible for the above pattern. Not only does the pattern repeat in a perfectly regular fashion, there is also structure, a degree of order, within the 31-node repeat unit. As a consequence of this order, we need fewer than 31 bits to describe the pattern. Let's see if we can find out the amount of bit reduction.
Have a careful look at the picture. Do you notice a pattern, some rule that applies? I give you a hint: pick a filled spot (blue disk). It doesn't matter which one. Out of the two nearest neighbor spots in the row above, how many are occupied? Now take another occupied spot, and again check the two neighboring spots immediately above it. How many are occupied? Repeat this until you have satisfied yourself there are no exceptions to the rule you have discovered.
Now repeat this for an empty spot. Check several such spots. You can distinguish two scenarios, right? What rule emerges?
Ok, if you have given this sufficient thought, you have discovered that the pattern is formed by a XOR (exclusive-or) rule: the occupancy of each spot in the hexagonal pattern is the XOR of the occupancy of the two spots immediately above it. This observation changes the determination of the entropy of this pattern dramatically. If you carefully consider the implication of this rule on the bit content of the pattern, you come to the conclusion that the above pattern can only contain five bits of information. This is visualized in below figure.
In short, if you specify 5 bits in a row for the 31-spot repeat pattern, you have determined the starting value of the repeat pattern, and you can use the XOR rule to fill the rest of the pattern. So we come to the conclusion that the entropy (the 'independent bit content') of the pattern is 5. In other words: the dynamics in below figure defines a lossless compression algorithm that describes the whole figure in only 5 bits.

Five bits are enough to specify the full pattern. Starting from five known occupancies, the gray disks (indicating unknown content of the spots) disappear under repeat application of the XOR rule.
A more physical way of looking at this is to observe that we are dealing with a one-dimensional dynamical system for which the spatial dimension runs from left to right, and time from top to bottom. Such discrete dynamical systems are referred to as 'cellular automata'. To specify the full dynamics of a cellular automaton, you need to describe only a suitable starting state. For the cellular automaton represented in the above figures, the starting state for the full 31-spot pattern consists of only five bits. This is in line with what we observe in real life. Entropy is an extensive property: it scales with the spatial volume of the system under consideration, not with its spacetime volume. So we have found a perfectly acceptable answer that relates to the entropic scaling behavior of real systems.
Well, the answer might seem acceptable, fact of the matter is: it is wrong. The number 5 might be closer to the truth than the number 31, but it is still way off.
It is true that defining five spots leads to a complete pattern, but what we have failed to take into account is that these five spots can have arbitrary occupancy. In the example shown, we have assumed all five starting spots to be occupied. However, you can change this into any other combination of empty and occupied spots, provided at least one is occupied. Each time you change the five-spot starting pattern, the same total pattern emerges, but each time shifted in a different way.
So we arrive at the shocking conclusion that the above binary pattern contains no information. You do not need to specify any of the spot occupancies. If you know nothing more than that we are dealing with a 31-spot XOR dynamics, you can reconstruct the whole picture.
This all might seem trivial, but we have to conclude that we are dealing here with nothing less than a model for holographic degrees of freedom. A toy model, yet a valid representation of holographically reduced entropy in a dynamical system.
We are used to the fact that when generated by a deterministic dynamics, the information contained in a two-dimensional pattern of pixels is not encoded in a two-dimensional pixel area, but in a one-dimensional row of pixels. However, when you look at the first figure, you see a holographic binary pattern with degrees of freedom that are 'thinned out' as if dictated by a further dimension reduction. The pattern is not encoded in a one-dimensional row of bits, but in a 'zero-dimensional group of bits'.
The above is the subject of the essay I submitted earlier this week to the FQXi/ScientificAmerican essay contest 'Is Reality Digital or Analog?' If this blog entry wets your appetite: have a look at the essay. It goes much deeper into the matter, yet I tried hard to keep the essay understandable also to non-physicists. Reading it, you might learn a thing or two about dual descriptions, path sums, and... the holographic nature of physical reality. Enjoy!
PS. Will keep you informed about the fate of my essay. Till mid March, you can discuss and rate the essays submitted to the contest.* Your ratings will determine which 35 essays will make it to the finals. You will notice that many essays (including my own) are quite speculative in character. That really is the nature of contests like these. Whilst you are at the FQXi site, you might want to have a look at the winning essays from the two earlier contests (here and here) * This requires a valid e-mail address.





Comments