Now, the title of this post is catchy enough that many of you may have come here to know the wonders of experimental physics, but I wish to warn you: although I kept the following explanation at a level which should be accessible to anybody who knows what conservation of momentum is, explaining why the Goldhaber experiment is so phenomenal requires delving into details and many will get confused -- or even worse, bored!--, before reaching the end...

Anyway, if you decided to take the ride, buckle up and here we go! 

The first steps toward understanding the weak interaction

During the fifties, physicists were busy trying to understand weak interactions of elementary particles. At the time, the first accelerators were starting to produce evidence for the existence of many new unexpected particles. One used to smash protons against targets, and study the bodies produced downstream. Many new "resonances" were thus found as peaks in the distribution of the combined invariant mass of (some of) the final state particles: mass is a well defined attribute of a particle, and it can be reconstructed by measuring energy and momentum of all the bodies created in the particle's disintegration.

Physicists were hoping that by studying the properties of these new found bodies they could understand the details of the weak interaction, the one which governed the decay of the neutron and of many other "strange" particles - strange because they were produced copiously (and thus with high probability) by the strong interaction, but were slow (due to the weakness of the interaction responsible) to disintegrate (so something that happened with low probability). 

Enrico Fermi, with brilliant intuition, had already laid down in the thirties the correct formalism for making theoretical calculations of the decay rate of these particles, but had ignored the fact that the weak interaction violates a symmetry of nature called Parity, a fact that was only postulated much later, by Lee and Yang in 1956. That fact was demonstrated soon afterwards by Wu and her collaborators at the National Bureau of Standards. There, the experimentalists observed a clear anisotropy in the direction of emission of decay electrons from radioactive Cobalt 60 isotopes, kept at low temperature and with their spins aligned along the direction of a strong magnetic field.

To continue my description, I now need to take a detour and introduce you to three different concepts: parity, helicity, and the transformation properties of different mathematical objects in relativistic quantum mechanics. You think you can't take it? Well, give it a try!

1. Parity

What is the parity of an interaction? This is a great question I need to answer before I can take you through Goldhaber's experiment. Parity is in general a number connected with the symmetry properties of a function. If by exchanging x by -x your function f(x) remains identical in value, f(x)=f(-x) and we say it has positive parity. If, on the other hand, you get f(-x)= -f(x), the function has negative parity. And if none of the above applies, then f(x) has no definite parity. 

Physical interactions such as electromagnetic ones -well studied and understood already in the fifties, thanks to the contributions of many geniuses among which it is impossible not to mention Richard Feynman and Julian Schwinger-- are supposedly conserving the parity of a physical state, and in quantum mechanics a physical state is described by a wave function. This is a complex mathematical object. An interaction will transform that wave function into a new one, and we can describe this mathematically if we describe the wave function as y(x) and the interaction as a quantistic operator O. Then y'(x) = O y(x) means that the operator O, acting on the state y, transforms it into a new state y'. 

Where am I getting? Well, if a wave function has definite parity (positive or negative), then the parity operation will return the same object multiplied by +1 or -1, depending on its parity: e.g. for a positive parity state y(x), we have Py(x) = y(x), and for a negative parity one we have Py(x) = -y(x). That wavefunction is then said to be an eigenstate of the parity operator, and +1 or -1 is the corresponding eigenvalue. 

Now suppose you apply an electromagnetic interaction to y(x), which is an eigenstate of positive parity. Whatever the operator describing the interaction is (call it O), it better do something like Oy(x) = y'(x) when, again, Py'(x) = y'(x): the application of O has turned y into an y' which still is an eigenstate of P: this says that Parity is conserved by electromagnetic interactions.

Until 1956 it was considered outlandish to imagine that parity could be violated by physical interactions. So much so that two newly discovered particles, the tau and the theta, were found with equal mass, spin, and other properties, but they were observed to have opposite parity due to their different decays. The temptation to say that these were one and the same particle which sometimes decayed one way and sometimes the other way was strong but the prejudice was stronger, and they were believed to be distinct particles for a while. But then came Lee, Yang, and Wu...

2. Helicity

Elementary particles can be characterized by a quantity called spin. Spin is an intrinsic angular momentum, and if measured in units of the reduced Planck's constant it has a magnitude that can only exist as zero or as multiples of 1/2: s = 0, 1/2, 1, 3/2, and so forth. But spin is a vector - more precisely, an axial vector - so it has a direction. Now, if you take a particle moving along some direction and you measure the projection of its spin in that direction, you will get as a result +s or -s. Helicity is just the sign of that number you get. "Right-handed" is a positive helicity, and "left-handed" is a negative helicity.  Easy? Well, yes, but wait a moment. 

Is helicity a useful quantity in particle physics? Yes and no. Imagine you see an electron whizzing by, and you know it has negative helicity. The electron may be going very fast, but it is a massive particle, so it travels at les  than the speed of light. Hence its speed does not prevent you from imagining to follow it until you overtake it. And if you do, the helicity of that electron will now be measured opposite than it was before, because you are now moving faster than it along the direction you have measured helicity along, so the electron now appears to move in the opposite verse... but its spin hasn't changed direction. By moving faster than the electron, you have changed its helicity! 

Helicity is only strictly conserved, and thus a descriptive quantity, of particles that have zero mass, because zero-mass particles move at the speed of light, and you cannot overtake them! This trick is only possible for few bodies in the subnuclear world: photons, gluons, and -until we discovered that this was not the case- neutrinos. Neutrinos were thought massless until they were found to have one, albeit very tiny. For the purpose of weak interaction studies, we can however consider them completely massless in the rest of this post.

Now, the parity violation of weak interactions can be enshrined by the fact that neutrinos exist in only one of their two possible helicity states. But which one? Are neutrinos left-handed or right-handed? We will get back to this problem very soon.

3. Symmetry properties of vectors

What we call a "scalar" quantity is a number, and numbers do not change when you subject them to translations, reflections, or rotations in space. An example of a scalar quantity is the scalar product of two vectors. Say you have a vector P and you multiply it by itself: the result is a scalar, P^2, a number. Instead, a vector quantity has different transformation properties. E.g., if you rotate by 180 degrees a vector, you get it to change verse. 

There are two kinds of vectors: polar and axial ones. Momentum P is a polar vector: if you take a reflection of P through a mirror parallel to it, P will not change. Instead, an axial vector such as angular momentum J changes verse! That is because J is the vector product of two polar vectors, J = R x P. The figure below will convince you of the fact.

Now, the parity operation consists in taking the mirror image of an object and rotate it by 180 degrees along an axis perpendicular to the mirror. If you do this to both P and J, that both change verse under 180 degree rotations, you get that P ends up flipping, while J stays the same. P and J have opposite transformation properties under the parity operation - this is why they are distinguished by the term "polar" or "axial".

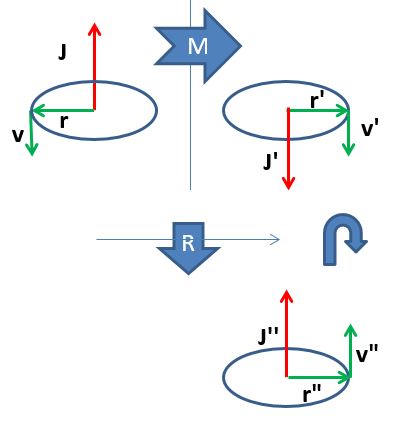
Above: an axial vector J, such as the product of radius r and velocity v in a circular motion, flips sign by mirror inversion M, so that the combination of M by a rotation R changes its verse: it flips by parity operation.

Now, while P^2 is a scalar quantity as we said above, if we take the scalar product of P and J we get a pseudoscalar quantity. Given that P is inverted by parity, but J isn't, the product JP will change sign under parity inversion. A pseudoscalar is an oddball of a number! 

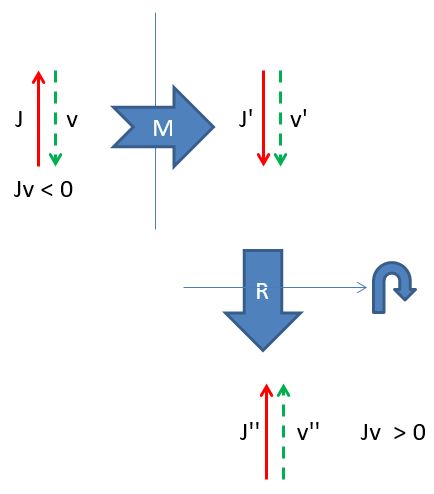
Above, the product of J and v (angular momentum and velocity) flips sign when the vectors are subjected to a parity inversion.

So now you know - until 1956, physicists thought that physical laws responsible of transformations of physical systems retained their parity unchanged - the measurable quantities of a system could not change if you took a parity inversion. This, by the arguments we have made above, implied that the quantum operators that produced those transformations could not contain pseudoscalar terms - as those would flip under parity.

Operators and their transformation properties

The quantum operators responsible for electromagnetic (EM) interactions obeyed the above rule: the interaction was a "vector" one, in the sense that EM operators had vector properties. Originally physicists had tried to model weak interactions in perfect analogy with electromagnetic ones, because the latter had been understood astoundingly well. This was Fermi's "V" formalism, where V stands for vector: weak interactions were described by operators that transformed as vectors under Lorentz group rotations.

But now, if weak interactions violated the parity symmetry, Fermi's "V" formalism had to be modified. Two options were borne by experimental data: the interaction was either "V-A" or "S-T", these letters identifying the symmetry properties of the interaction potential: V for (polar) vector, A for axial vector, S for scalar, and T for tensor. If the interaction was V-A, then beta decay (the mechanism through which radioactive atoms decay, by transforming one neutron into a proton, an electron, and a neutrino) had to produce (anti)neutrinos which spinned clockwise; if the interaction was S-T, the antineutrinos would all spin counterclockwise. In both cases, the mixing of V and A, or S and T, terms in the weak interaction Lagrangian is the essence of why that interaction violates the Parity symmetry.

But how does this come about? We discussed above vectors and axial vectors, but we also discussed how their product becomes a scalar or a pseudoscalar quantity. Now, the Lagrangian contains terms that describe how particles propagate, and if these include the sum of V and A terms, then whenever you compute the rate of a physical process you end up squaring those terms. You then face a calculation of the kind (V-A)*(V-A), which if explicitated returns terms proportional to V*A. These are pseudoscalars, and violate parity. The same result would occur if you ended up with (S-T)*(S-T) terms.

It would be soo nice for me to be able to explain more in detail the above calculation, but this post is getting too long... So you will have to trust me on the above.

Measuring the helicity of neutrinos

Neutrinos are the most elusive particles we know. They are enormously copious in the universe, since the fusion mechanisms in the star cores emit gazillions of them. But they almost never interact with matter when they traverse it: their cross section, or probability of yielding an interaction, is so tiny that most of the time they cross the entire earth unscathed. So if they do not interact, they cannot be seen! We in fact detect particles by observing their interaction with matter. How then, thought Goldhaber and company, can we be so clever as to measure their spin, which is an elusive property to begin with?

The first intuition that the trio had was to search for a radioactive element that decayed by beta interaction emitting neutrinos of energy E and turn into another nucleus which would immediately de-excite by emitting a photon of energy similar to E. This fact was crucial for the scheme they were developing: they wanted to convert the mission impossible of measuring the neutrino spin to that of measuring the spin of the photon emitted by de-excitation of the daughter nucleus, as the polarization of photons - their spin - is something they knew they could measure. But how to pull this off?

Enter Europium 152, a radioactive isotope with quite peculiar characteristics. Fast to decay, it has zero total angular momentum (J=0: no net spin), and transmutes into excited Samarium by capturing one of its own inner electrons, thereby emitting a neutrino in one direction, and a Samarium nucleus in the other -the two bodies balancing the total impulse, thanks to conservation of momentum.

Excited Samarium has a total spin J=1 (in units of Planck's constant), and is also quite peculiar: it decays into its fundamental state - it de-excitates - by emitting a 960 keV photon so quickly (in 0.07 picoseconds) that its direction of motion has no time to be lost by thermal effects, even in a solid sample of Europium. This is an important observation for the experiment, as we will be relying on it for the measurement! As for the photon, which is a particle endowed with one unity of spin, it may have spin either aligned or anti-aligned with its own direction of motion, and, due to conservation of angular momentum, certainly aligned with the original spin of excited Samarium. 

Now, if the photon has been emitted along the direction of motion of excited Samarium, its spin will be aligned with the original spin of the neutrino emitted in the original decay of Europium, and it will have the same sign! This means that if we measure the photon spin properties, we infer the neutrino's spin properties. Bingo number 1!

But how can we select those photons emitted exactly in the direction of excited Samarium? Bingo number 2 was to realize that the photons do not possess all the energy of the de-excitation of Samarium: when the photon is emitted, the Samarium atom recoils, keeping to itself some of the energy released in the form of kinetic energy. So these photons, when they encounter another atom of Samarium, will not be able to pump it back to the excited state, UNLESS... Unless the photon was emitted by Samarium traveling in the same direction, thereby being "kicked forwards", doppler-shifted to higher energy. So it will be only those photons that are able to do resonant scattering with a Samarium nucleus. Bingo number 3 was to recognize the fact that the momentum acquired by the Samarium nucleus in the decay of Europium is roughly equal to the amount necessary for the photon to gain just the needed kick forward!

To summarize: if you want to measure the neutrino's spinning property (AKA its polarization) you just need to measure the polarization of those photons which do resonant absorption by Samarium atoms (those that were kicked forward).

Ok, but how did they do that? That was easy! Photons with energy of about a MeV have different interaction properties in a sample of iron which is magnetized parallel or antiparallel to the photons direction. That is due to the electrons in the iron being more likely to absorb photons of a given spin if their spin is antiparallel to it.

The end result? Take a sample of Europium 152, place it before a block of magnetized iron. Place a sample of Samarium behind it, and an instrument to detect the secondary radiation from de-excitation of the Samarium undergoing resonant scattering (a photomultiplier will do). Count the ticks of the tube, turn the iron by 180 degrees, count again. The larger counts will identify more transmitted photons, which will tell about their polarization! Easy as pie!!

The picture above shows a sketch of the experimental apparatus. A small source of Europium is placed in the niche at the left, immersed in a block of magnetized iron. a big lead shielding prevents photons from reaching th photomultiplier directly from the Europium source. The rectangles labeled "Sm2O3" identify a ring of Samarium oxide, which is used as the scatterer, where photons can do resonance absorption. The photomultiplier tube is connected to a sodium iodide scintillating crystal, which records the photon signal.

Here is the original paper (click on the gif thumbnails to enlarge):

Page 1

Page 2

Page 3

Now you be the judge. Was this not one of the cleverest things you've ever heard about?

Indeed, through inventiveness and cleverness, Goldhaber and company designed and carried out one of the most extraordinary experiments in modern Physics. Reducing the measurement of one of the most elusive properties of subnuclear matter to a mere count of ticks of a photomultiplier tube is an enormous achievement! The neutrino is spinning counterclockwise, antineutrinos are clockwise. The interaction is V-A: a fundamentum of Particle Physics.