With large citation databases such as Google Scholar at everybody's fingertips, a citation impact analysis of an individual takes no more than a few mouse clicks. As a result citations statistics is increasingly seen as a practical means to determine scientific impact of physicists. The citation statistics of individual researchers is commonly summarized in the form of a citation index, a single number that is transparent, objective and supposed to describe the total impact of the individual's published work.
Tens of different indices have been defined, yet they all have their flaws. In fact, they are flawed to an extend that really makes me wonder. Much better indices can easily be defined, so why has no-one come up with improved, yet simple and elegant citation indices?
Flawed Indices
Before I describe such new indices, I need to explain what is wrong with existing citation indices. I will focus on the Hirsch or h-index, as this is by far the most widely used citation index.A scientist can claim to have a h-index of N if (s)he has authored or co-authored N papers that each have been cited at least N times. Defined this way, the h-index attempts to measure both the productivity and impact of the published work of a scientist. However, the h-index is really geared towards scientists with an established career in publishing papers. It is largely meaningless for researchers who are most affected by it: scientists early in their careers. The generic example to explain this is to imagine a new Einstein. A young scientist who went through a 'miraculous period' and published three groundbreaking papers. This person is applying for an academic position. The committee checks the h-index of all candidates, and appoints the candidate with the highest h-index: 'Mr. Mediocre'', a young scientist who co-authored five useless papers that each got quoted five times, mainly by his co-authors and a few other impact-less scientists in his immediate network.
What went wrong?
The young Einstein published only three papers, and then focused on a challenging new problem that she hopes to crack in a few years time. The three papers in the meantime attracted several hundred citations each, but the h-index is blind to that statistics. Per definition, the h-index of the young Einstein with a total of three publications is capped to three. Her competitor, Mr. Mediocre, has attracted far fewer citations, but these were spread over more publications, and therefore resulted in a higher h-index.
Later in their careers, provided she will secure an academic position and be able to continue publishing, it is virtually certain that the young Einstein will bypass Mr. Mediocre also in terms of their h-indices. In other words, the h-index does a decent job in measuring total lifetime achievement. However, that doesn't help young Einstein right now. As useful as it might be for measuring full career achievement, for scientists early in their careers, the h-index measures mostly the quantity rather than the quality of their publications.
Can we define a citation index that is more useful to rank the impact of researchers who are still early in their career? The answer is yes, and it is really easy to come up with such indices. I will give you two examples: first the simple Einstein or E-index, and secondly the more sophisticated Pythagorean or P-index.
The Einstein Index
The E- (Einstein) index is geared to correct the young Einstein problem. This index is defined as the sum of the citations to the three most cited publication of the person whose citation impact is being measured. It should be clear that this index does a much better job in comparing the young Einstein with Mr. Mediocre. Mr. Mediocre with five publications that each are cited five times reaches an E-index of 15. The young Einstein, however, amasses an E-index score of many hundreds. In contrast to the h-index, the E-index does measure quality rather than quantity of publications.Now you might reason "Ok, this E-index seems to have advantages for early career science impact measurement, but does it not in general lead to unrealistic rankings? Would scientist with one 'lucky article' not get on top?"
This is not the case.
Using Google Scholar, I calculated the Einstein index of a number of well-known theoretical physicists.* I have not attempted to generate a complete overview, but the list does include many famous theoreticians including a bunch of Nobel laureates. Below table shows the result.
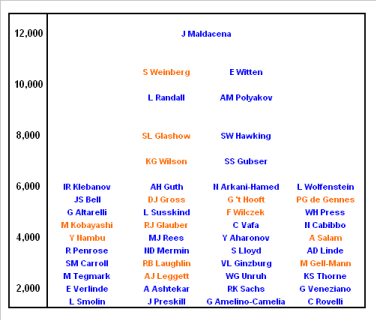
Einstein-indices for well-known theoretical physicists and cosmologists. The Einstein index is plotted vertically, and each scientist is listed by the search term used in Google Scholar. Nobel laureates are shown in amber, others are listed in blue.
There might be a few surprises in the picture, but the total ranking looks more than reasonable. The bottom level of this table is chosen at an Einstein index of 1,500 corresponding to three papers attracting 500 citations each. A more than respectable amount. Erik Verlinde, who featured prominently in this blog last year, weighs in at a level of 2,000. Nobel laureates typically have an Einstein index of around 3,000 or higher. Physics and cosmology blogger Sean Carroll has entered the bottom end of this level which, without any doubt, makes him the physics blogger with the highest Einstein index. At levels above 6,000 we see true giants emerging. Well-known names like Stephen Hawking reside at this level. Lay people often expect him to head the list, but most physicists will not be surprised to see that folks like Ed Witten are well ahead of Hawking. Also ahead of Hawking, and highest scoring female is Lisa Randall at a score approaching the 10,000 mark. Just ahead of Randall and highest scoring Nobel laureate is Steven Weinberg. Weinberg is accompanied at a 10,500 Einstein index level by Ed Witten. Flying high above these two giants and heading the list is Juan Maldacena with an astonishing Einstein index of 12,000. It is reassuring to see him come out in the top spot. If there is any contemporary theoretical physicist who deserves the title 'Einstein of today', it's him.** As many of you will know, Maldacena is the guy who demonstrated how nature can be holographic, en-passant proving Hawking wrong on the fundamental nature of Hawking radiation. For a popular account of his amazing work on the AdS/CFT correspondence, you should consult his Scientific American article.
Zipf And The Pythagorean Index
For the people listed, their most highly cited papers constitute 40 - 70 % of their Einstein indices. In other words, the feared 'single highly cited outlier' effect is absent. A person who has published a highly cited paper will publish more of these during his/her career. This is in line with what one may expect based on the observed Zipf distribution of citations. This Zipf distribution states that when all publications of a scientist are ranked from top cited paper to lowest cited paper, the citations per paper are inversely proportional to their rank (1 to n) on the list. Averaged over the whole group, this Zipf distribution indeed nicely emerges from the data used to construct above plot. It turns out that on average the second (third) ranking paper for a given person attracts 2.2 (3.1) times fewer votes than his/her top ranking paper.This brings us to a more advanced citation index: the P- or Pythagorean index. This index results when fitting the citation count distributions for a given person to a Zipf distribution. I will not go into any of the math here, but for those interested: the Pythagorean index follows when performing a least squares analysis to citation counts that are close to the Zipf distribution. Note that there is no 'wiggle room' and no possibility for tweaking. The Pythagorean index follows from a rigorous analysis. It is what it is.*** The Pythagorean index that results takes the shape of an equation that lends it its name. For a given person, the square of his/her Pythagorean index equals the sum of the squares of the number of citations to each of his/her papers. So a person with two publications that attracted 4 and 3 citations respectively, will have a square P-index of 16 + 9 = 25, or a P-index of 5.****
The Pythagorean index can be seen as the distance in 'citation space' between the scientist being checked, and a layperson who has not published any scientific work. This index nicely eliminates the various issues pestering the h-index and related indices. Most importantly, just like the Einstein index, the Pythagorean index places emphasis on the few most highly cited publications of a person. It is therefore an indicator that can be applied to measure early career achievements.
Tiny Indices, Overhyped Messages
When you have some time to spare, you might want to cross-plot the Einstein and Pythagorean indices for a group of scientists of your choice. A narrow cloud of data points will be the result. It follows that for most practical purposes the simple straightforward Einstein index suffices.The result is that anyone can check the scientific impact of each and every scientist: in Google Scholar look up the name of the person you are interested in, and add the number if citations to his/her highest scoring papers. This gives you a huge advantage when confronted with over-hyped messages. An example to illustrate the point. Left, right and center you witness blogs and articles appearing about a 'surfer dude' who has constructed an 'exceptionally simple theory of everything'. You take a look at his paper and at first sight you are not particularly impressed. Are you wrong in your judgment? Do you overlook somehow the brilliance of this new theory? Should you invest in studying this paper in much more detail? You decide to check the Einstein index of its author A.G. Lisi. You arrive at an Einstein index of 63. You decide to spend your valuable time on something that is likely more rewarding.
"Wait a second!" I hear you say, "a low Einstein index of the author does not mean this work is crap. It could as well be that the whole physics community is ignoring this brilliant new kid on the block."
Well, let me tell you a little secret: the global physics community consists of many thousands of folks who have build their careers on showing new avenues and proving others wrong. If there is some merit in a new idea, you can be guaranteed that hordes of these folks jump on it and try to extend it and apply to new areas. If this doesn't happen even after more than three years, chances are the idea has little merit.
Tiny Indices, Huge Egos
Scientists like to measure and are fond of numbers. So they must have embraced citation analysis as the next best thing since sliced bread.Forget it.
As unbelievable as it may seem to outsiders, scientists are prone to human emotions. More particularly, the egos of scientist are as inflatable as that of anyone else, and probably a wee bit more. That means that the vast majority of scientist must be convinced their work is better than that of an average scientist. Picture such a scientist vanity-checking his/her Einstein index, and ending up with some miserable double digit figure. Would it be possible that this person falls victim to cognitive dissonance reduction symptoms? Well, I guarantee you this person will use all his/her polemic skills in trying to prove citation analysis being wrong.For this person I have a little advice at the bottom of this blog post.
Now, I am not saying here that citation analysis is a magic silver bullet. It should be clear that it can be nothing more than a starting point in a judgment process. An objective and practical starting point, but only a starting point. Hirsch, in his paper on the h-index that has emerged as his top-cited paper, makes the remark:
"Obviously a single number can never give more than a rough approximation to an individual’s multifaceted profile, and many other factors should be considered in combination in evaluating an individual. This and the fact that there can always be exceptions to rules should be kept in mind especially in life-changing decision such as the granting or denying of tenure."
Wise words that also apply to the indices discussed here. One last thing: whether you like it or not, citation analysis is not going to disappear. The thing is: the people who decide on grants love it. It creates a level playing field, and gives them an objective measure. So, accept the wide availability of citation statistics as a given, and focus on delivering top-notch research. Once in a while you will strike gold. If not: be honest to yourself: are you really the creative genius you think you are? Is science your real destination?
Notes
* You can do this yourself in Google Scholar. Just enter the name of the scientist whose citation impact you want to determine, and hit the return key. You will see a list of publications for this scientist, together with the number of citations these publications attracted. The top-cited paper appear on top. Now just select the three papers with the highest citations (make sure you include only research papers and no books) and add up the three numbers. This gives you the E-index.** it is not only his top ranking in terms of the Einstein index, that makes Maldacena the right candidate for the title 'Einstein of today'. Like Einstein, Maldacena is an immigrant to the US, and like Einstein he works at the famous Institute for Advanced Study at Princeton. If not literally then at least figuratively speaking, Maldacena is sitting at Einstein's desk.
*** This is not the case for the h-index which leaves a lot of room for 'tuning'. For instance the h-index can be modified into a 10h-index that is claimed to better balance between measuring quality and quantity.
**** A useful generalization is to correct for co-authorship and divide the squares of the citations to each of the papers by the number of authors.
----------------------
The Hammock Physicist on: What's Wrong With E=m.c2?, What's Wrong With 'Relativity'? Entropic Gravity, Entropic Force, Shut Down LHC?, Game Theory, Metric Vs Imperial, Big Bang, Dark Energy, Chaos And Time's Arrow, The Grand Arena, Square Root Of The Universe, Physics In A Nutshell, The Longest Path, Hotel Boltzmann, Quantum Telepathy, Quantum Viruses, QHD, Fibonacci Chaos, Counting A Black Hole, Entropic Everything, God, Godel, Gravity, Holographic Automata





Comments